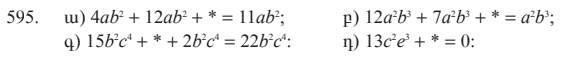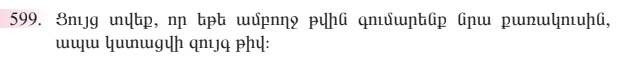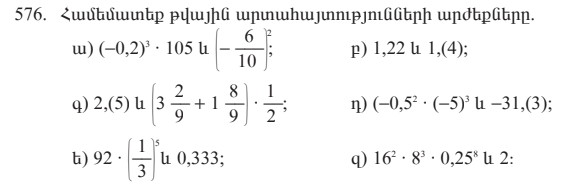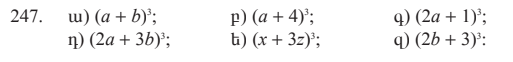1․ Ի՞նչն են անվանում երկու անհայտով երկու առաջին աստիճանի հավասարումների համակարգի լուծումը։
Երկու անհայտով երկու առաջին աստիճանի հավասարումների համակարգի լուծումը անվանում են այդ հավասարումների ընդհանուր լուծման կարգավորիչներ կամ լուծումների զույգ, որը բավարարում է երկու հավասարումներին միաժամանակ։

2․ Ի՞նչ է նշանակում լուծել համակարգը։
Նշանակում է գտնել նրա բոլոր լուծումները կամ ապացուցել, որ լուծումներ չկան:

3․ Ընտրել x+y=15 հավասարմանը բավարարող բնական թվերի զույգ:

• (17;−2)
• (0;15)
• (−9;−6)
• (−6;21)
• (3;5)
• (13;2)

4․ Ընտրել այն հավասարումը, որին բավարարում է (2;1) թվազույգը:

• 15x−12y=3
• 6x+8y=1
• 7x+3y=10
• 4x−3y=7
• 6x−2y=4
• 10x−11y=9

5․ Համակարգի հավասարումներում անվանել գործակիցները և ազատ անդամները.

6․ Հանդիսանում է արդյո՞ք (2;1) թվազույգը հետևյալ համակարգի լուծում:

7․ Ցույց տալ, որ (1;2) թվազույգը համակարգի լուծում է.

8․ Ցույց տալ, որ (-2;1) թվազույգը համակարգի լուծում չէ.

9․ Տրված է հավասարումների հետևյալ համակարգը՝

Հայտնի է, որ (−6;9) թվազույգը նրա լուծումն է: Որոշել a և b գործակիցները:

Առաջադրանքներ։

1․ Որոշիել ax+2y=16  հավասարման a գործակցի արժեքը, եթե հայտնի է, որ (−2; 4) թվազույգը այդ հավասարման լուծում է:
-2a+8=16
-2a=16–8
-2a=8
8/-2=-4

2․ Տված հավասարումներից y-ը արտանայտել x-ով:

ա) 2x+y=6
y=6-2x
բ) 3x+y=7
y=7-3x
գ) x+y-8=12
y=12-x
դ) y+2=6x
y=6x-2
ե) 3x+2y=9
2y=9-3x
զ) -4x+2y=13
2y=13+-4x

3․ Տված հավասարումներից x-ը արտանայտել y-ով:

ա) x-y+5=0
x=y-5
բ) 2x-3y+9=0
2x=3y-9
գ)15x+y-8=0
15x=-y+8
դ) x+3y-15=0
x=-3y+15
ե) 7x+y=6
7x=6-y
զ) -4x+y=-19
-4x=-19-y

1․ ա) Ո՞ր հավասարումն են անվանում երկու անհայտով առաջին աստիճանի հավասարում: Բերեք օրինակներ:
ax+by+c=0 (1)

Հավասարումը, որտեղ a, b, c-ն տված թվեր են, ընդ որում a և b թվերից գոնե մեկը տարբեր է զրոյից, իսկ x-ը և y-ը անհայտներ են, անվանում են երկու անհայտով առաջին աստիճանի հավասարում:

3x+2y-1=0

 բ) Ի՞նչն են անվանում ax+by+c=0 հավասարման լուծում, որտեղ a և b գործակիցներից գոնե մեկը հավասար չէ զրոյի:

ax, by, c  արտահայտություններնանվանում են (1) հավասարման անդամներ: Ընդ որում c թիվն անվանում են ազատ անդամ:

2․ Քանի՞ լուծում ունի x-y+1=0 հավասարումը:
Անվերջ

3․ Տրված a, b, c թվերով կազմեք առաջին աստիճանի երկու անհայտով հավասարում.

ա) a=5, b=4, c=-2;

x+y+(-2)=7

բ) a=0, b=-3, c=4;

x-y+4=1

գ) a=0, b=2, c=-1;

x+y-(-1)=1

դ) a=-5, b=-1, c=0:

x-y+0=-4

4․Պարզել  x−2y+5=0 երկու անհայտներով գծային հավասարման a, b և c գործակիցները:
a=1, b=-2, c=5։

5․ Ցույց տալ, որ (1;-1), (5;-7), (-3; 5) թվազույգերը 3x+2y-1=0 հավասարման լուծումներն են:

1.

3x+2y-1=0

3 x 1+2 x (-1)-1=0

3-2-1=0

2.

3x+2y-1=0

3 x 5+2 x (-7)-1=0

15-(-14)-1=0

3.

3x+2y-1=0

3 x (-3)+2 x 5-1=0

-9+9-1=0

6․ 8x+4y−8=0 գծային հավասարման մեջ որոշել x=0 արժեքին համապատասխանող y-ի արժեքը:
8x+4y-8=0

8 x 0+4 x 2-8=0

0+8-8=0

y=2

7․ 13x+5y=26 գծային հավասարման մեջ գտնել y=0 արժեքին համապատասխանող x -ի արժեքը:
13x+5y=26

13 x 2+5 x 0=26

26+0=26

x=2

8․Տրված է երկու փոփոխականներով 3x−7y+22=0 գծային հավասարումը: Օգտագործելով այն` արտահայտել x  փոփոխականը մյուս փոփոխականի՝ y-ի միջոցով:
3x−7y+22=0

3 x (-33)+7 x 11+22=0

-99+77+22=0

x=-33, y=11

9․ Որոշել ax+8y=20 հավասարման a գործակցի արժեքը, եթե հայտնի է, որ (−4;−4) թվազույգը այդ հավասարման լուծում է:
ax+8y=20 

-13 x (-4)+8 x (-4)=20

55+(-32)=20

a=-13

10․ x+2y−24=0 հավասարման լուծումներից գտնել այնպիսի թվազույգ, որի թվերից առաջինը 2 անգամ մեծ է երկրորդից:
x+2y−24=0 

12+2 x 6-24=0

(12+12)-24=0

x=12, y=6, հետևաբար առաջին թիվը 2 անգամ մեծ է երկրորդից։

Թեմա՝ Կրկնողություն

1. Հաշվել
ա) 3³ ա)3*3*3=27
բ) 8² բ)8*8=64
գ) 6⁴ գ)6*6*6*6=1296
դ) 1²⁰⁰⁰ դ)1*1*1*1*1*1*1*1*1…=1


2. Գրել ցուցչային տեսքով՝
ա) 2 ⋅ 2 ⋅ 2=2³
բ) 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5=5⁶
գ) 2³ ⋅ 2 ⋅ 2=2⁵


3. Գրել 10 աստիճանի  տեսքով՝
ա) հարյուր հազար 10⁵
բ) մեկ միլիոն 10⁶
գ) մեկ միլիարդ 10⁹


4. Հաշվել 10³ և 6² թվերի արտադրյալը։
10³*6²=1000*36=36000


5. Համեմատել ա) 2³⁰ < 2³¹ թվերը, բ) 7¹⁰ < 9¹⁰ թվերը։

 6․ 5, 2, −5 թվերից որո՞նք են հետևյալ հավասարման լուծումները.
ա) x — 2 = 0, x=2
բ) 2x -10  = 0, x=5
գ) 3x +15 = 0  x=-5

7. –3, 12, 1, –5 թվերից որո՞նք են նշված հավասարման լուծում.
ա) x + 3 = 0, x=-3
բ) 2x – 25 = –1, x=12
գ) 3y + 10 = 1, x=-3
դ) 5y + 7 = 2 (y – 1) + 12 x=1


8. Ուղղանկյան պարագիծը 48 սմ է։ Գտնել ուղղանկյան կից կողմերի գումարը։
48:4=24

9․ Դպրոցի երկու դասարանում կա 54 սովորող, ընդ որում ՝ մի դասարանում մյուսից 4 սովորողով ավելի։ Քանի՞ սովորող կա դասարաններից յուրաքանչյուրում։ 

x+4+x=54
2x=50
x=25
x+4=29

S1=b*a=ba
S2=b*a=ba
S3=4b*a=4ba
S4=4b*a=4ba
S5=b*2a=2ab
S6=5b*2a=10ba
S7=4b*2a=8ba

ա)V=40 km S=40 T=1ժամ
բ)T=21,2կմ/ժ S=1,2km V=20km

ա)a=4,2մ s=4մ b=200սմ
բ)b=8կմ s=1,6կմ a=20մ

ա)p=s/r²
բ)r=c/2p

ա)S=10*t
բ)S=v*5

ա)4*b*c
բ)a*b*2

ա)
բ)
գ)
դ)
ե)
զ)

ա)-6a²b<6a²b
բ)3a³x³y=3a³x³y
գ)-a³b⁴c³<1/4a²b⁴c⁴
դ)7/3 a³x³y³c³>4/3 a³x⁴y³c²

ա)9>8
բ)32 >25
գ) 0,25 >0,16
դ)1,1 < 4,1
ե)16/25 < 25/16
զ․(1 1/3)³>2,4²
է․0,5²<0,5³
ը․(4/5)²<(4/5)³
թ․(-0,3)²>(-0,4)²

ա.(1/2)⁵<(3/4)³
բ.(1/3)⁵<(1/9)²
գ.(-1/2)⁵>(-3/4)³
դ.(-2/5)³<(-1/2)⁵
ե.(-1/3)²*(-1/2)>(-1/6)²
զ.(-1/5)²*(-3/4)>(-3/4)²
է.1 1/3-1/3*(1 1/4-1/9*(1 1/2)²)<1
ը.1/2*((2 1/3)²-31*(1/3)²)-1>1

ա.(-0,5)²,-16,1<4
բ.(-5)³,0,1<2,1³
գ.8*(-1/2),8*(-1/2)²>8:(-1/2)

ա․(-0,2)³*105<(-6/10)²
բ․1,22<1(4)
գ․2()5<(3 2/9+1 8/9)*1/2
դ․(-0,5²*(-5)³)>-31(3)
ե․92*(1/3)⁵>0,333
զ․16²*8³*0,25⁸<2

ա)ab
բ)(a+b)²=a²+ab+b²
գ)(a+b)³=a³+ab+b³
դ)a²+b²=a²b²
ե)a³+b³=a³b³
զ)2a*2b=4ab
է)3a*3b=9ab
ը)a²*3b=3a²b
թ)

ա)x³+3x²y+3xy²+y³
բ)x³+3x²1+3×1²+1³
գ)x³+3x²+12x+8
դ)3³+33²y+33y²+y³

ա)a³+3a²b+3ab²+b³
բ)a³+3a²4+3a4²+4³
գ)2a³+32a²1+32a1²+1³
դ)2a³+32a²3b+32a3b²+3b³
ե)x³+3x²3z+3x3z²+3z³
զ)2b³+32b²3+32b3²+3³

ա․ab
բ․
գ․
դ․

ա.x³-3x²y+3xy²-y³
բ.x³-6x²+3x-1
գ.x³-6x²+12x-8
դ.x³-9×2+27x-27

ա.a³+3a²b+3ab²+b³
բ.a³-3a²b+3ab²-b³
գ.a³+6a²+12a+8
դ.a³-6a²+12a-8
ե.a³+9a²+27a+27
զ.a³-9a²+27a-27
է.a³+12a²+48a+64
ը.a³-12a²+48a-64
թ.8a³+12a²b+6ab²+b³
ժ.a³-6a²b+12ab²-8b³
ի.27a³+54a²b+36ab²+8b³
լ.27a³-54a²b+36ab²-8b³

ա․2a²+2a+1-2a-2+1=2a²
բ․m²-2mn+n²+2mn-2n2+n²=m²
գ․
դ․

25/100, 75/100 ,14 5/100,125/1000, 875/1000, 1 75/10000

ա․0,526471>0,524671
բ․2,076812<2,076813
գ․0,247459<0,347459
դ․7,127586>7,1278

ա․4/7

ա․0,5+0,345=0,845
բ․1,3+0,416=1,716
գ․4,2+1,304=5,504
դ․12,4+0,012=12,412
ե․1,47-0,84=0,63
զ․5,12-2,0904=3,0304
է․6,45-0,079=6,389
ը․15,2-2,0904=13,2904

ա․85/1
բ․68/1
գ․90/1

ա․4,5-27,5=-23:2,3=-10+2,3=-7,7
բ․2,2-1,44=0,84*5=4,20
գ․0,4-0,45=0,05+1,24=1,29*5=6,45:3,5=1
դ․1230*0,01=12,3-4,8=7,5:2,5=0*1,6=0

533.1/3-1/2=-1/6
2/7-4/5=-18/35
-2/8-7/9=19/36

534.1/2+1/3=5/6
17-1/3=50/3
1278-2/7=8944/7
1/2-3=-5/2

536.

536.25*7*8=1400
13*12*25=3900
2*1/2+3*1/3=2
1/7*7-1/6*6=0
36:3*(1/3-2*1/4)=-2
(75-100*1/2)*1/25=1

ա․17/2-15/4=19/4 19/1*2/1=38/1=35
բ․4/1-7/6-25/4=109/12 109/12:1/2=109/6
գ․18/5-3/2+12/5=50/30
դ․59/8-19/4+7/2=49/8
ե․13/5-25/2-11/5=173/10 173/10:2/1=173/10*1/2=173/20
զ․20/3-48/5+31/2=3/30 3/30:3/1=1/3*1/1=1/3

ա.5/7*3/1=15/7-21/4=60-147=-17/28 -87/28:7/1=-87/28*1/7=-87/196 -87/196:3/1=-87/196*1/3=-87/588 -87/588+91/28=-87+1911=1824/588
բ.5/1*4/1=20/1-49/4=80-49=31/4 31/4:7/9=31/4*9/7=279/28:6/1=279/28*1/6=279/168 279/168+81/8=279+1701=1980/168

ա․5/14-8/21=15-16=-1/42
բ․
գ․
դ․

ա.(-1/2)⁵*45=-45/32
բ.(-3)¹⁶*(1/9)⁷=9
գ.4²⁰/8¹³=2
դ.2¹⁰*25⁴/4000000=100

ա․2*3²⁰-5*3¹⁹=3¹⁹*(2*3-5)=3¹⁹*1=9¹⁸3¹⁹/9⁹=9⁹
բ․
գ․
դ.