Գիտելիքների ստուգում:

1)ա)11 բ)21 գ)0,6
2)ա)20 բ)7 գ)54 դ)50 ե)0,06
3)ա)> բ)< գ)>
4)ա) բ) գ)
5)ա)x=324 բ)x=121 գ)լուծում չունի
6)ա)x=2 բ)x=100 գ)x=7

Առաջադրանքներ։

1․ Լուծել հավասարումները․

ա)D=36+4*4*0=36 x₁=-6+6/4=0 x₂=-6-6/4=-3
բ)D=16-4*4*1=0 x₁=4+0/8=0,5 x₂=4-0/8=0,5
գ)D=-4*3*-12=144 x₁=0+12/6=2 x₂=0-12/6=-2
դ)D=25-4*1*6=1 x₁=5+1/2=3 x₂=5-1/2=2
ե)D=9-4*6*-1=33 x₁=-3+√33/12 լուծում չունի
զ)D=196-4*5*-3=256 x1=-14+16/10=2/10 x2=-14-16/10=30/10=3

2․Լուծել հավասարումները․

ա)D=16-4*4*-3=64 x₁=-4+8/8=4/8=0,5 x₂=-4-8/8=12/8=1,5
բ)D=144-4*9*-5=324 x₁=-12+18/18=6/18 x₂=-12-18/18=30/18
գ)D=49-4*2*3=25 x₁=-7+5/4=-0,5 x₂=-7-5/4=3
դ)D=1-4*4*-3=49 x₁=-1+7/8=6/8 x₂=-1-7/8=8/8=1
ե)D=400-4*4*9=256 x₁=-20+16/8=-0,5 x₂=-20-16/8=4,5
զ)
է)լուծում չունի
ը)լուծում չունի

3․ Լուծել հավասարումները․

ա)D=25-4*2*3=1 x₁=-5+1/4=-1 x₂=-5-1/4=1,5
բ)D=36-4*1*9=0 x₁=-6+0/2=-3 x₂=-6-0/2=3
գ)D=9-4*1*-4=25 x₁=-3+5/2=1 x₂=-3-5/2=4
դ)լուծում չունի
ե)D=64-4*0,5*-18=100 x₁=-8+10/1=2 x₂=-8-10/1=18

4․ Լուծել հավասարումները․

ա)D=81-4*2*9=9 x₁=-9+3/4=-1,5 x₂=-9-3/4=3
բ)D=1-4*3*-4=49 x₁=-1+7/6=6/6=1 x₂=-1-7/6=8/6
գ)D=1-4*3*-4=49 x₁=-1+7/6=6/6=1 x₂=-1-7/6=8/6
դ)D=1-4*2*-10=81 x₁=-1+9/4=2 x₂=-1-9/4=2,5

Հարցեր և առաջադրանքներ։

1․ Ո՞ր հավասարումն է կոչվում քառակուսային։
ax²+bx+c=0 տեսքի հավասարումը, որտեղ a -ն, b -ն և c -ն տրված թվեր են, և a≠0, անվանում են քառակուսային (քառակուսի) հավասարում:

2․ Ինչպե՞ս են հաշվում քառակուսային հավասարման տարբերիչը։

3․ Ո՞ր հավասարումն է կոչվում թերի քառակուսային։
Քառակուսային հավասարումը կոչվում է թերի, եթե b և c թվերից գոնե մեկը հավասար է զրոյի:

4․ Կազմել ax²+bx+c=0 քառակուսային հավասարում, եթե նրա գործակիցները հավասար են․

ա)3x²+4x+5
բ)3x²-2x+6
գ)x²-x+2
դ)-x²+3x-2x

5․ Հաշվել քառակուսային հավասարման տարբերիչը․

ա)a=2 b=-3 c=-5
բ)a=1 b=5 c=1
գ)a=9 b=-6 c=1
դ)a=1 b=1 c=1

6․ Ստուգել՝ 0 թիվը հավասարման արմա՞տ է․

ա)այո
բ)ոչ
գ)ոչ
դ)ոչ
ե)այո
զ)ոչ

Լուծել հավասարումները․

ա)x=-1;+1
բ)
գ)1
դ)x=0;-3
ե)x=3;-2
զ)x=-5;7
է)x=0;0,5
ը)
թ)
ժ)

7․ Լուծել հավասարումները․

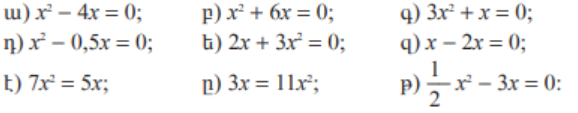
ա)x=0;4
բ)x=-6;0
գ)x=-1/3;0
դ)x=0;0,5
ե)x=-2/3;0
զ)
է)x=0;5/7
ը)x=0;3/11
թ)x=0;6

8․ Լուծել հավասարումները․

ա)x=-√3;√3
բ)x=-√5;√5
գ)x=-√3;√3
դ)x=-√50;√50
ե)x=-√3/2;-√3/2
զ)լուծում չունի
է)x=-48;48
ը)x=-5,6;5,6
թ)x=-√200;√200

Հարցեր և առաջադրանքներ։

1․ Ո՞ր բազմանդամն են անվանում քառակուսային եռանդամ։
ax²+bx+c տեսքի բազմանդամը, որտեղ a -ն, b -ն և c -ն տրված թվեր են, և a≠0, անվանում են քառակուսային եռանդամ:

2․ Ինչի՞ է հավասար քառակուսային եռանդամի տարբերիչը։
D=b²−4ac թիվն անվանում են ax²+bx+c քառակուսային եռանդամի  տարբերիչ կամ՝ դիսկրիմինանտ:

3․ Հետևյալ արտահայտություններից ո՞րն է հանդիսանում քառակուսային եռանդամ: Ընտրիր ճիշտ պատասխանի տարբերակը:

ա) 14x²−3x−1
բ) 4x−5
գ) x+5/2x−3

4․ Արդյո՞ք բազմանդամը քառակուսային եռանդամ է․

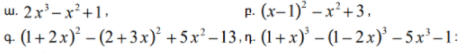
ա)ոչ
բ)ոչ
գ)այո
դ)ոչ

5․ a-ի ի՞նչ արժեքի դեպքում է բազմանդամը քառակուսային եռանդամ․

6․ Նշել քառակուսային եռանդամի ավագ, միջին և ազատ անդամները։

7․ Կազմել քառակուսային եռանդամ տված գործակիցներով։

ա)3x²+4x+5
բ)3x²-2x+6
գ)x²-x+2
դ)-x²+3x-2x

8․ Գրել քառակուսային եռանդամի a, b և c գործակիցները․

ա)a=6 b=1 c=-2
բ)a=1 b=-1 c=7
գ)a=-5 b=3 c=-1
դ)a=-1 b=1 c=1

9․ Առանձնացնել լրիվ քառակուսին․

10․ Հաշվել քառակուսային եռանդամի տարբերիչը․

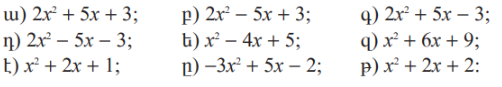
ա)D=1
բ)D=1
գ)D=49
դ)D=49
ե)D=-4
զ)D=0
է)D=0
ը)D=1
թ)D=-4

Առաջադրանքներ։

1․Լուծել անհավասարումները;

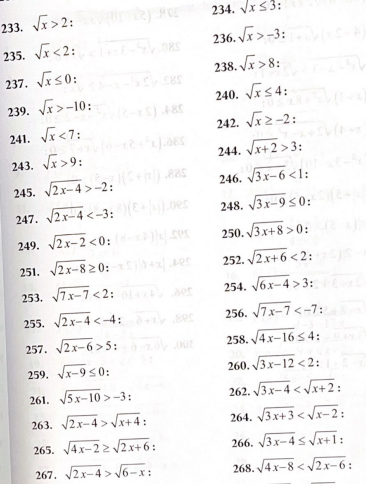
233)x∈[4;+∞)
234)x∈[0;9]
235)x∈[0;4)
236)x∈[9;+∞)
237)x=0
238)x∈(64;+∞)
239)x∈(0;+∞)
240)x∈(0;16)
241)x∈(0;49)
242)x∈(0;+∞)
243)x∈(81;+∞)
244)x∈(7;+∞)
245)x∈(2;+∞)
246)x∈(0;7/3)
247)x∈(0;0,5)
248)x=3
249)
250)x∈(-8/3;+∞)
251)x∈(4;+∞)
252)x∈(-3;-1)
253)x∈(1;11/7)
254)x∈(13/6;+∞)
255)
256)
257)x∈(31/2;+∞)
258)x∈(4;8)
259)x=9
260)x∈(4;16/3)
261)x∈(2;+∞)
262)
263)
264)
265)
266)
267)
268)

2․ Լուծել անհավասարումները։

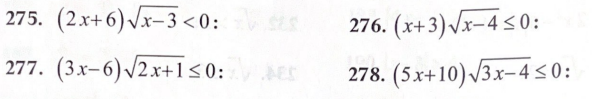
275)լուծում չունի
276)լուծում չունի
277)լուծում չունի
278)լուծում չունի

Հարցեր և առաջադրանքներ։

1․Ո՞ր հավասարումներն են կոչվում իռացիոնալ։
Եթե հավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա այդպիսի հավասարումը անվանում են իռացիոնալ:

2․ Ինչպե՞ս են լուծում պարզագույն իռացիոնալ հավասարումները։
Այսպիսով, իռացիոնալ հավասարումը լուծելու համար պետք է՝

1) այն բարձրացնել քառակուսի,

2) լուծել ստացված հավասարումը,

3) կատարել ստուգում՝ դեն նետելով ավելորդ արմատները,

4) գրել վերջնական պատասխանը:

3․ Լուծել հավասարումները։

ա)x=9
բ)x=0
գ)x=1
դ)x=0,5
ե)x=0,5
զ)x=-1
է)x=44/3
ը)x=48/5
թ)x=25

4․ Լուծել հավասարումները։

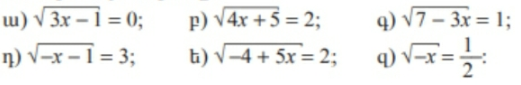
ա)x=1/3
բ)x=-1/4
գ)x=2
դ)x=-10
ե)x=8/5
զ)x=-1/4

5․ Լուծել հավասարումները․

249)x=4
250)x=9
251)x=25
252)x=4
253)x=0
254)x=81
255)x=64
256)x=4
257)x=25
258)x=0
259)x=4
260)x=11
261)x=6
262)x=20
263)x=6
264)x=6
265)x=25
266)x=9
267)x=4.5
268)x=10
269)x=1
270)x=9/5
271)x=10/3
272)x=1
273)x=6
274)x=0,5
275)x=7/2
276)x=7
277)x=-4
278)x=10
279)x=-1
280)x=3/4

1․ Պարզեցնել արտահայտությունը․

ա)5√2
բ)√2
գ)-4√a
դ)(a-3)√x
ե)√a
զ)-√2

2․ Համեմատել արտահայտությունների արժեքները առանց արմատը հաշվելու։

ա)>
բ)>
գ)<
դ)<
ե)<
զ)>

3․ Պարզեցնել արտահայտությունը․

ա)1-√3
բ)5–√5
գ)√2-√3

4․ Հայտարարում ազատվել արմատանշանից։

ա)√2+1
բ)√3+1
գ)
դ)
ե)
զ)

5․ Կրճատել կոտորակը․

6․ Արտադրիչը տանել արմատանշանի տակ․

Առաջադրանքներ

1․ Ընտրիր ճիշտ հատկությունները:

• √a+√b=√a+b
• √a²=a, a≥0
• √a: √b=√a:b
• √a⋅a =a, a≥0
• √a⋅a=a²

2․ Հաշվել․

ա)6
բ)12
գ)20
դ)35
ե)90
զ)560

3․ Հաշվել․

ա)20
բ)18
գ)30
դ)48
ե)220
զ)105
է)210
ը)630
թ)154

4․ Հաշվել․

ա)√2
բ)√9
գ)√x
դ)√3

5․ Հաշվել․

ա)8
բ)15
գ)30
դ)70
ե)20
զ)90
է)800
ը)5000

6․ Հաշվել․

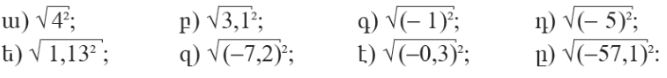
ա)4
բ)3,1
գ)1
դ)5
ե)1,13
զ)7,2
է)0,3
ը)57,1

7․ Արտադրիչը դուրս բերել արմատանշանի տակից․

ա)√2/3
բ)3/4
գ)√40/9
դ)√72/5
ե)5/√2
զ)√5/2
է)x√x/3
ը)√7a/4b²
թ)
ժ)
ի)
լ)

8․ Արտադրիչը դուրս բերել արմատանշանի տակից

Առաջադրանքներ։

1․ Հաշվել քառակուսի արմատը․

3,4,5,7,9,11,15,17,19,24,26,22,27,31

2․ Հաշվել

ա)3
բ)9
գ)5
դ)9
ե)6
զ)2
է)4
ը)1
թ)0,13

3․ Հաշվել

ա)18
բ)10/3
գ)1
դ)1,2
ե)0,09
զ)4900
է)3
ը)1/100
թ)5,2

4․ Համեմատել

ա)>
բ)<
գ)<
դ)<
ե)>
զ)>
է)>
ը)>
թ)>

5․ Հաշվել

ա)2
բ)3
գ)13
դ)17

6․ Հաշվել

ա)30
բ)18
գ)2
դ)6
ե)2
զ)-3,1

7․ Հաշվել

ա)7/9
բ)8/10
գ)4/3
դ)3/2
ե)13/29

8․ Գտնել  արտահայտության արժեքը՝  0.4√0.16+1/2⋅√256
8,16

Առաջադրանքներ։

1․Որոշել y=x² պարաբոլի ճյուղերի ուղղվածությունը:  

• Ճյուղերն ուղղված են դեպի վերև
• Ճյուղերն ուղղված են դեպի ներքև

2․Գտիր y=x² ֆունկցիայի արժեքների բազմությունը: Ընտրել ճիշտ տարբերակը:

• Ֆունկցիան սահմանափակ չէ ներքևից
• Ֆունկցիան սահմանափակ չէ վերևից

3. Տրված է y=−x² ֆունկցիան: Ընտրել ճիշտ պատասխանը:

ա) y_max=−1 բ) y_max=1 գ) y_max=0

4. Տրված է f(x)=−x² ֆունկցիան: Հաշվել
f(−1)=-1
f(−5)=-25
f(0)=0
f(2)=-4
f(4)=-16

5. Արդյո՞ք  A(3; 8) կետը պատկանում է  y=x²  ֆունկցիայի գրաֆիկին:

ա) չի պատկանում
բ) պատկանում է

6. Արդյո՞ք  A(x; y) կետը պատկանում է  y=x² ֆունկցիայի գրաֆիկին, եթե
ա) x=1,y=2 ոչ
բ) x=3, y=9 այո
գ) x=-2; y=4 այո
դ) x=0,4; y=1,6 ոչ

7. Համեմատել թվային արտահայտությունների արժեքները՝
ա) 1,17² < 1,18²
բ) 2,31² < 2․33²

8. y=x²  ֆունկցիայի հանար համեմատել y₁ և y₂ , եթե
ա) x₁=0,5 x₂=0,6
բ) x₁=9,2 x₂=8,5

ա)y₁=0,25 y₂=0,36
y₁<y₂
բ)y₁=84,64 y₂=72,25
y₁>y₂