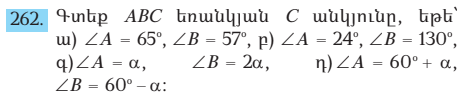
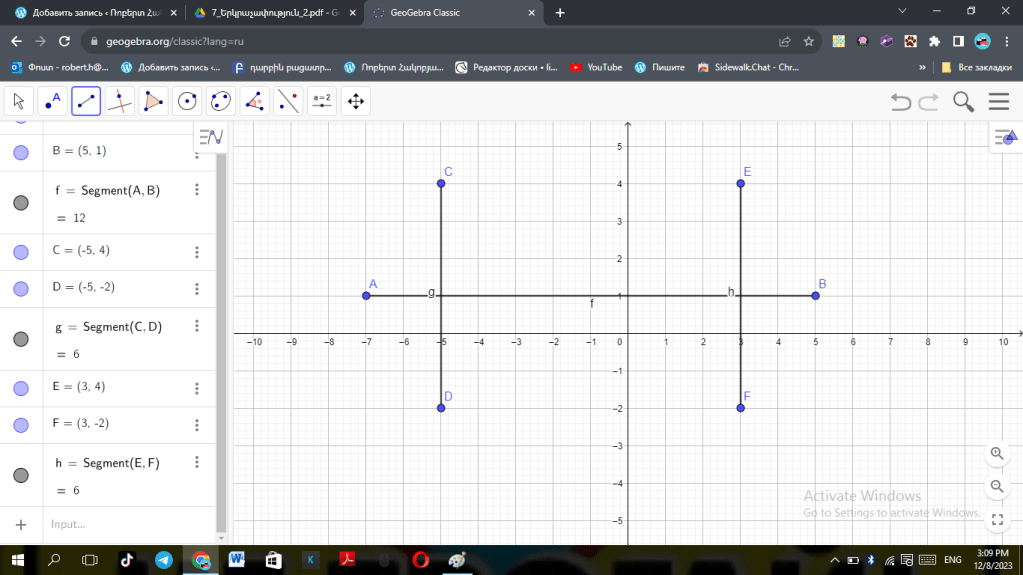
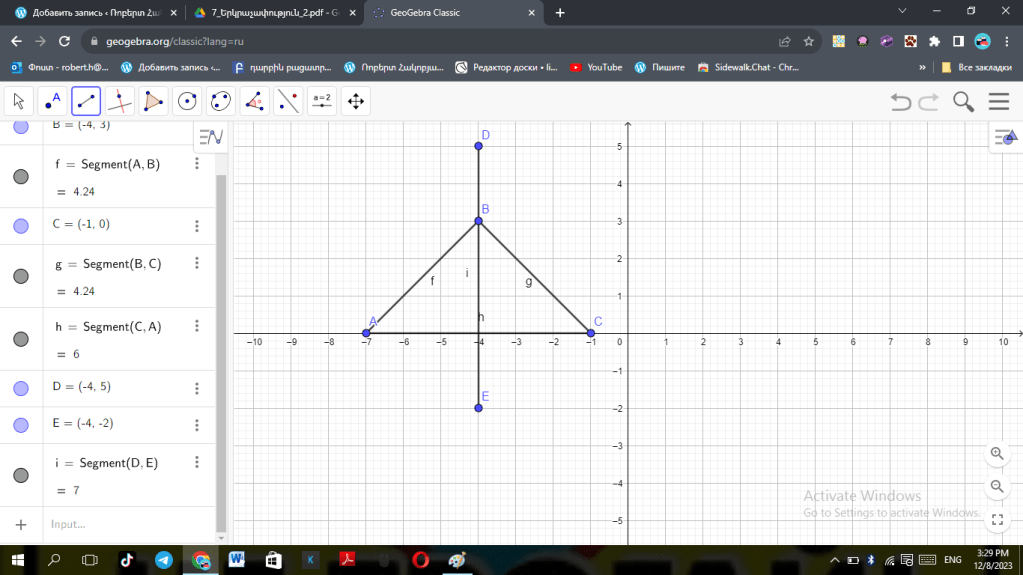
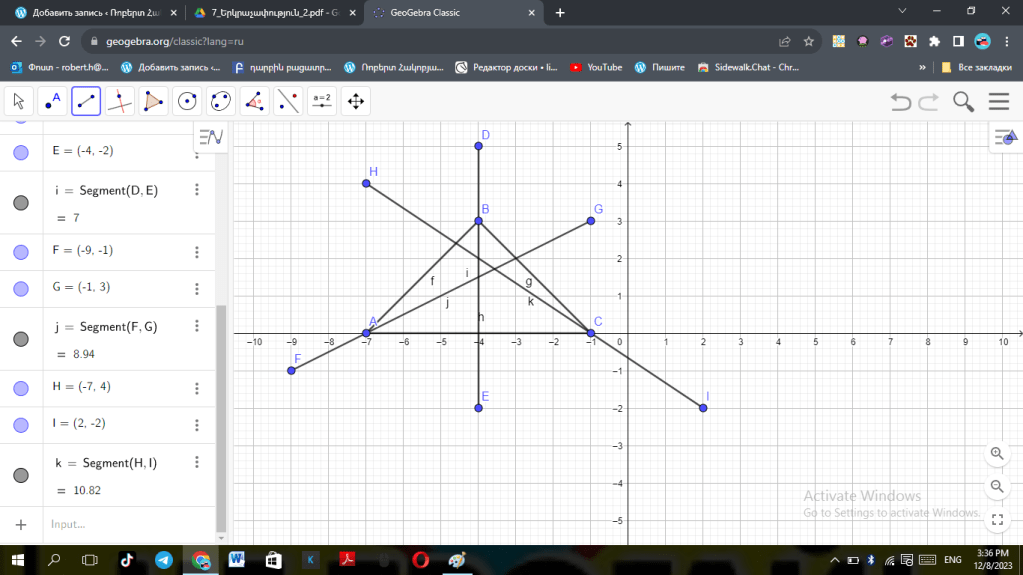
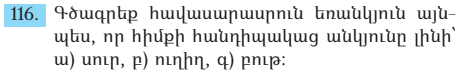
ԱՔՍԻՈՄՆԵՐ և ԹԵՈՐԵՄՆԵՐ
01.02.2024

ա)

բ)

գ)

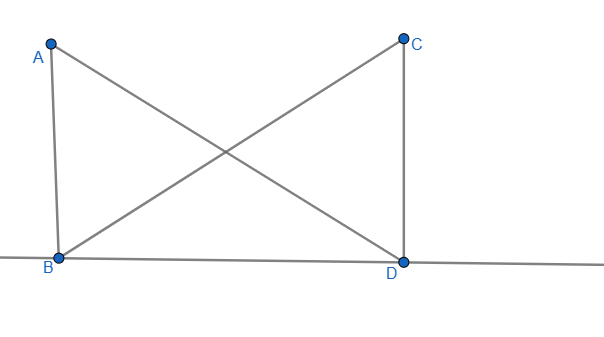
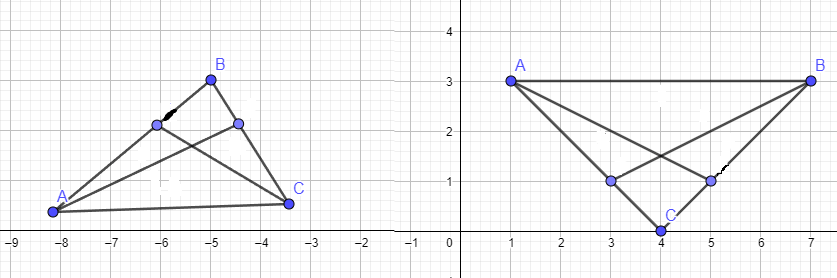
AB=CD

BD Կողմը ընթանուր է իրենց կազմված անկյուները հավասար են

<BDA, <CDE
Հակադիր են ուրեմն հավասար են ապա ըստ եռանկյուների հավասարեն առաջինի հայտանիշի ▲ABD=▲CDE

P=2x+2x+x=50

2x+2x+x=5x

5x=50

5x:50=10

10×2=20

AB=20

CB=20
AC=10

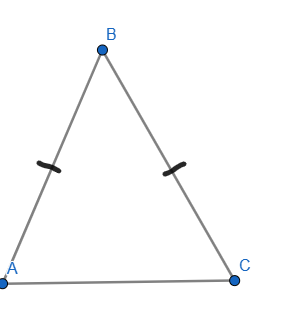
P=x+x+x+9

3x+9=45

3x=36

x=12,12,21

BC+CD+BD=45

45:3=15

x+x+15=40

2x=40-15=25

x=12,5

BC=15 AB=12,5

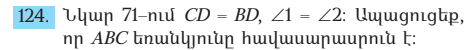
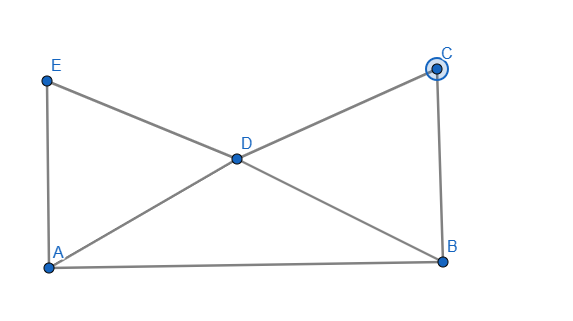
Քանի որ CD=BD AD ընդհանուր է <1=<2 ապա ըստ եռանկյունների հավասարության առաջին հայտանիշի 🔺ABC=🔺ADB ապա հետևում է որ 🔺ABC=հավասարասրուն է։

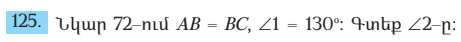
Քանի որ <1 և ❤ կից անկյուններ են ապա <3=180-130=50 քանի որ 🔺ABC հավասարասրուն եռանկյուն է ապա <3=<4=50 քանի որ <2 և <4 հակադիր են ապա <2=<4=50⁰

Բոլոր խնդիրների գծագրերը կատարում ենք geogebra ծրագրով։

86.

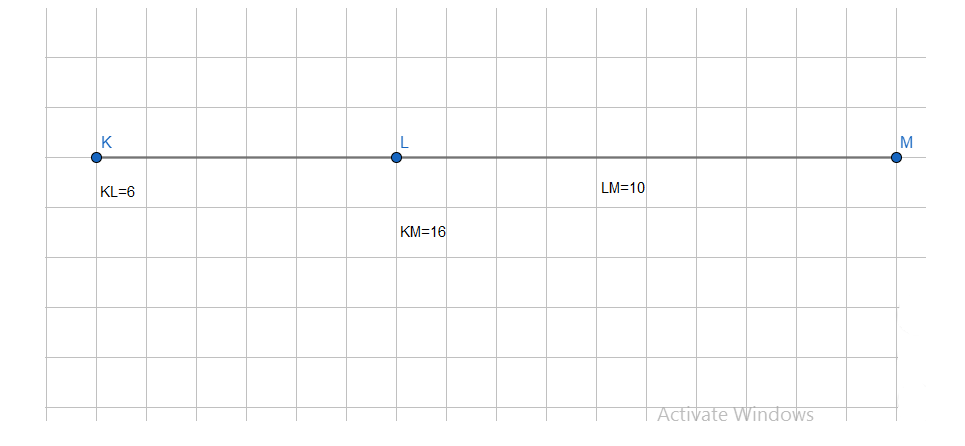
87.AB=2PQ=2AB PQ=QB AP+PQ+PQ/2 AP=Q-PQ-PQ

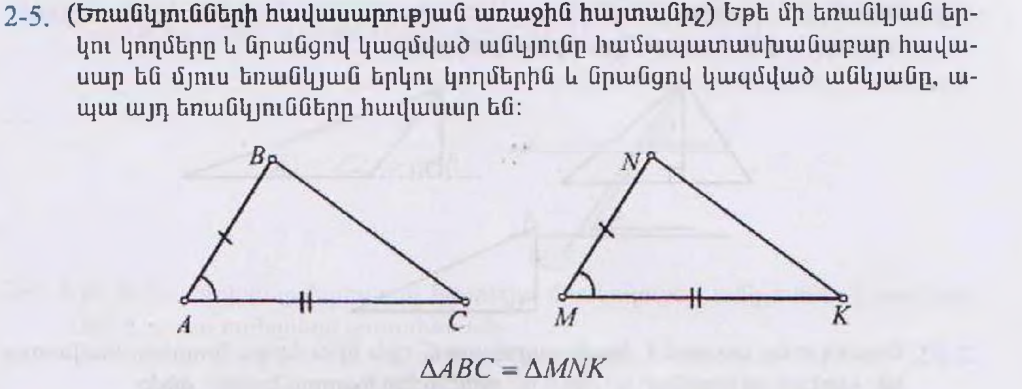
Առաջադրանքներ

1.Քանի որ ▲ABC=▲MNK
AB=MN=6
BC=NK=7
AC=MK=10

2.Քանի որ ▲ABC=▲MNK
<A=<M=40
<B=<N=60
<C=<K=80

3.Քանի որ ▲ABC=▲MNK
P▲ABC=P▲MNK=65

4.ABC =AB+BC+AC=10+5+13=28

5.MNK մեծ է ABC 8-ով

6.AB=22
BC=22
AC=11
P=55

7․AB=15
BC=15
AC=22
P=52

Տարբերակ 1։

1. Քանի՞ աստիճանով է պտտվում ժամացույցի րոպեների սլաքը 30 վայրկյանում:
   90-15
   x-0,5
   x=90*0,5:15
   x=3
2. a և b ուղիղների հատումից առաջացած կից անյումններից մեկը մյուսից մեծ է ինը անգամ։ Գտնել ուղիղների հատումից առաջացած բոլոր չորս անկյունները։
   x+9x=180
   10x=180
   x=18
   18*9=162
   18, 162, 18, 162
3. O կետից տարված են h, k, l ճառագայթները, ընդ որում՝ h⊥k: hk և kl անկյունների կիսորդներով կազմված անկյունը 600 է: Գտեք hl անկյունը:
   60-45=15
   hl=15+15=30
4. Հակադիր անկյունների գումարը հավասար է ուղիղ անկյան աստիճանին։ Գտնել հակադիր անկյունները։
   90:2=45
   180-45=135
   135, 45, 135, 45

Տարբերակ 2։

1. Քանի՞ աստիճանով է պտտվում ժամացույցի րոպեների սլաքը 1 րոպեում:
   90-15
   x-1
   x=90:15=6
2. k և l ուղիղների հատումից առաջացած կից անյուններից մեկը մյուսից մեծ է ութ անգամ։ Գտնել ուղիղների հատումից առաջացած բոլոր չորս անկյունները։
   x+8x=180
   9x=180
   x=20
   20*8=160
   20, 160, 20 ,160
3. O կետից տարված են h, k, l ճառագայթները, ընդ որում՝ h⊥k: hk և kl անկյունների կիսորդներով կազմված անկյունը 900 է: Գտեք hl անկյունը:
   90-45=45
   hl=45+45=90
4. Հակադիր անկյունների գումարը հավասար է փռված անկյան աստիճանին։ Գտնել հակադիր անկյունները։
   180:2=90
   180-90=90
   90, 90, 90, 90

Յուրաքանչյուր պնդում, որի ճշմարիտ լինելը հաստատվում է դատողությունների միջոցով, մաթեմատիկայում անվանում են թեորեմ: Այդպիսի դատողությունների ներկայացումը կոչվում է թեորեմի ապացուցում:

Թեորեմ

Եթե մի եռանկյան երկու կողմերը և դրանց կազմած անկյունը համապատասխանաբար հավասար է մյուս եռանկյան երկու կողմերին և դրանց կազմած անկյանը, ապա այդպիսի եռանկյունները հավասար են:

Ապացույցն ինքնուրույն (հետազոտական աշխատանք)

Թեորեմը կոչվում է եռանկյունների հավասարության առաջին հայտանիշ:

Առաջադրանքներ

1) Նկարում BC=AD, <1=<2:

ա) Ապացուցել, որ ΔABC=ΔACD:

Քանի որ եռանկյան երկու կողմերը հավասար են եռանկյունները հավասար են։

բ) Գտեք AB-ն և BC-ն, եթե AD=17 սմ և DC=14 սմ:

AB=14

BC=17

2) Նկարում OA=OD, OB=OC, <1=74⁰, <2=36⁰:

ա) Ապացուցեք, որ AOB և DOC եռանկյունները հավասար են:

բ) Գտեք <ACD-ն:

Լրացուցիչ

3) AC և BD հատվածները հատվում և հատման կետում կիսվում են: Ապացուցեք, որ ΔABC=ΔACD:

4) Նկարում AO=OC, <1=<2: Ապացուցեք, որ AB=BC:

5) CAD անկյան կողմերի վրա նշված են B և E կետերն այնպես, որ B կետն ընկած է AC հատվածի վրա, ընդ որում՝ AC=AD և AB=AE: Ապացուցեք, որ <CBD=<DEC:

Եռանկյունը բազմանկյուն է, որն ունի երեք կողմ։ Այլ կերպ այն կարելի է սահմանել որպես այնպիսի պատկեր, որը կազմված է միևնույն ուղղի վրա չգտնվող երեք կետերից, և այդ կետերը զույգ առ զույգ միացնող երեք հատվածներից։ Այդ կետերը կոչվում են եռանկյան գագաթներ, իսկ հատվածները՝ նրա կողմեր։ 

A, B, և C գագաթներով եռանկյունը հաճախ նշանակում են ΔABC: Այդ նույն եռանկյունը կարելի է նշել նաև այլ կերպ. օրինակ՝  ΔBAC, ΔCAB

Երեք անկյունները՝ <BAC-ն, <ABC-ն և <ACB-ն կոչվում են եռանկյան անկյուններ: Անկյունները նշանակվում են նաև մեկ տառով՝ <A, <B և <C:

Եռանկյան բոլոր կողմերի երկարությունների գումարը կոչվում է նրա պարագիծ:

Երկու պատկերներ, այդ թվում նաև երկու եռանկյուններ կոչվում են հավասար, եթե վերադրումով դրանք կարող են համընկնել:

Հավասար եռանկյունների մեջ համապատասխանաբար հավասար (այսինքն՝ վերադրելիս համընկնող) կողմերի դիմաց ընկած են հավասար անկյուներ, և ընդհակառակը՝ համապատասխանաբար հավասար անկյունների դիմաց ընկած են հավասար կողմեր:

ABC և A₁B₁C₁ եռանկյունների հավասարությունը նշանակվում է այսպես՝ ΔABC= ΔA₁B₁C₁

Առաջադրանքներ

1)ABC եռանկյան կողմը հավասար է 17սմ և հայտնի է որ բոլոր կողմերկ երկարությունները ամբողջ թվեր են։ Գտնել եռանկյան պարագիծը եթե AC կողմը կրկնակի մեծ է AB կողմից, իսկ BC կողմը 10սմ-ով փոքր է AC կողմից:        

AC=34
BC=24
BA=17
P=75                                                                     

2)Եռանկյան պարագիծը 48սմ է, իսկ կողմերից մեկը՝ 18սմ: Գտեք մյուս երկու կողմերը, եթե նրանց տարբերությունը 4,6սմ է:       

BA=18
AC=12,7
BC=17,3
P=48

3) ABC եռանկյան պարագիծը 15 սմ է: BC կողմը AB կողմից մեծ է 2սմ-ով, իսկ AB կողմը AC կողմից փոքր է 1սմ-ով: Գտեք եռանկյան կողմերը:
BC=6սմ
AC=5սմ
BA=4սմ

Լրացուցիչ

4) Եռանկյան կողմերի երկարությունները հարաբերում են ինչպես 5:12:13, իսկ փոքր կողմը 10 սմ է: Գտնել եռանկյան պարագիծը:

5) Եռանկյան մի կողմը 10 սմ է,մյուսը` երկու անգամ մեծ այդ կողմից, երրորդը՝ 5սմ-ով փոքր է երկրորդ կողմից: Գտնել եռանկյան պարագիծը:

6) Եռանկյան մի կողմը հավասար է 12 սմ, մյուս երկու կողմերի տարբերությունը 4սմ է, իսկ պարագիծը՝ 32սմ է: Գտնել եռանկյան կողմերը:

Եռանկյունը բազմանկյուն է, որն ունի երեք կողմ։ Այլ կերպ այն կարելի է սահմանել որպես այնպիսի պատկեր, որը կազմված է միևնույն ուղղի վրա չգտնվող երեք կետերից, և այդ կետերը զույգ առ զույգ միացնող երեք հատվածներից։ Այդ կետերը կոչվում են եռանկյան գագաթներ, իսկ հատվածները՝ նրա կողմեր։ 

A, B, և C գագաթներով եռանկյունը հաճախ նշանակում են ΔABC: Այդ նույն եռանկյունը կարելի է նշել նաև այլ կերպ. օրինակ՝  ΔBAC, ΔCAB

Երեք անկյունները՝ <BAC-ն, <ABC-ն և <ACB-ն կոչվում են եռանկյան անկյուններ: Անկյունները նշանակվում են նաև մեկ տառով՝ <A, <B և <C:

Եռանկյան բոլոր կողմերի երկարությունների գումարը կոչվում է նրա պարագիծ:

Երկու պատկերներ, այդ թվում նաև երկու եռանկյուններ կոչվում են հավասար, եթե վերադրումով դրանք կարող են համընկնել:

Հավասար եռանկյունների մեջ համապատասխանաբար հավասար (այսինքն՝ վերադրելիս համընկնող) կողմերի դիմաց ընկած են հավասար անկյուներ, և ընդհակառակը՝ համապատասխանաբար հավասար անկյունների դիմաց ընկած են հավասար կողմեր:

ABC և A₁B₁C₁ եռանկյունների հավասարությունը նշանակվում է այսպես՝ ΔABC= ΔA₁B₁C₁

Առաջադրանքներ

1)ABC եռանկյան կողմը հավասար է 17սմ և հայտնի է որ բոլոր կողմերկ երկարությունները ամբողջ թվեր են։ Գտնել եռանկյան պարագիծը եթե AC կողմը կրկնակի մեծ է AB կողմից, իսկ BC կողմը 10սմ-ով փոքր է AC կողմից:                                                                             

2)Եռանկյան պարագիծը 48սմ է, իսկ կողմերից մեկը՝ 18սմ: Գտեք մյուս երկու կողմերը, եթե նրանց տարբերությունը 4,6սմ է:       

3) ABC եռանկյան պարագիծը 15 սմ է: BC կողմը AB կողմից մեծ է 2սմ-ով, իսկ AB կողմը AC կողմից փոքր է 1սմ-ով: Գտեք եռանկյան կողմերը:

Լրացուցիչ

4) Եռանկյան կողմերի երկարությունները հարաբերում են ինչպես 5:12:13, իսկ փոքր կողմը 10 սմ է: Գտնել եռանկյան պարագիծը:

5) Եռանկյան մի կողմը 10 սմ է,մյուսը` երկու անգամ մեծ այդ կողմից, երրորդը՝ 5սմ-ով փոքր է երկրորդ կողմից: Գտնել եռանկյան պարագիծը:

6) Եռանկյան մի կողմը հավասար է 12 սմ, մյուս երկու կողմերի տարբերությունը 4սմ է, իսկ պարագիծը՝ 32սմ է: Գտնել եռանկյան կողմերը: