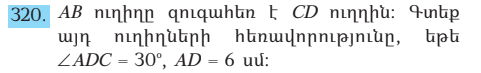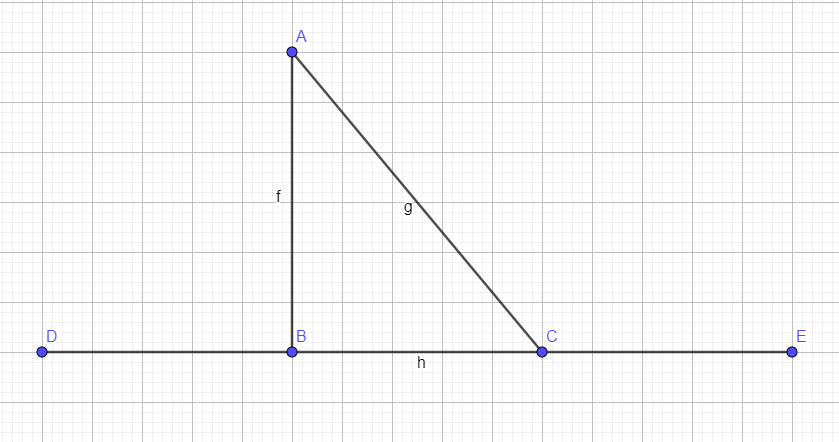
AB+AC=17
AC-AB=1
AC=1+Ab
AB+AC=17
AB+1+AB=17
2AB=17-1
2AB=16
AB=8

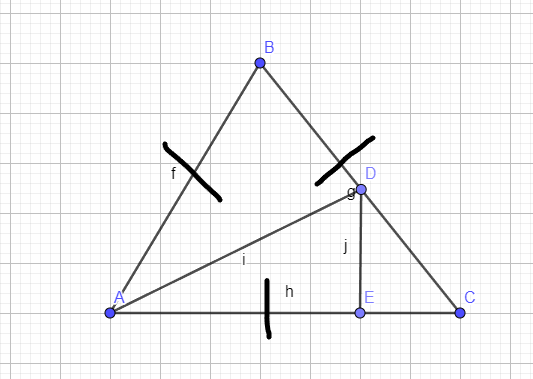
DE=6սմ
<A=<B=<C=60
<DAE=30
DE=AD/2
AD=12

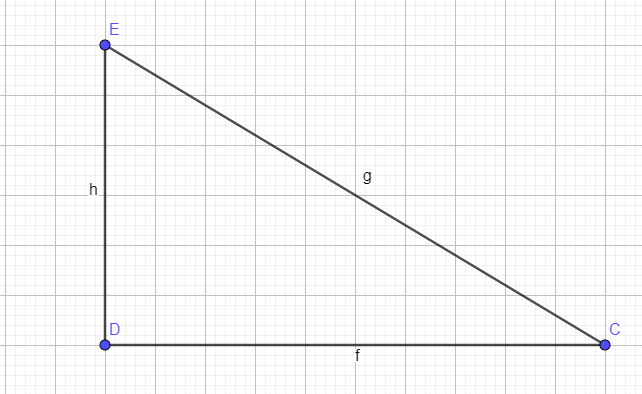
CE+CD=31
CE-CD=3
CE=3+CD
CE+3+CD
CD=14
CE=28
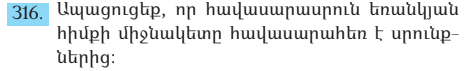
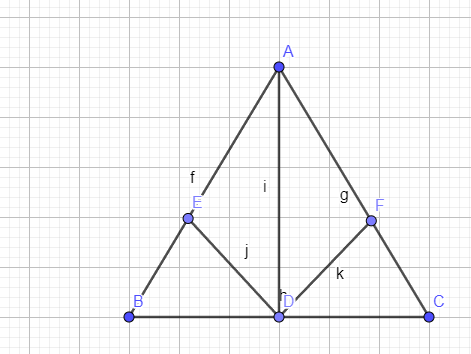
Քանի որ ABC եռանկյունը հավասարասրուն է ապա ըստ թեորեմի հավասարասրուն եռանկյան հիմքին տրարված կիսորդը նաև միջնագիծ է և բարձրություն => եռանկուն ABD=եռանկյուն ACD ապա BED=DFC

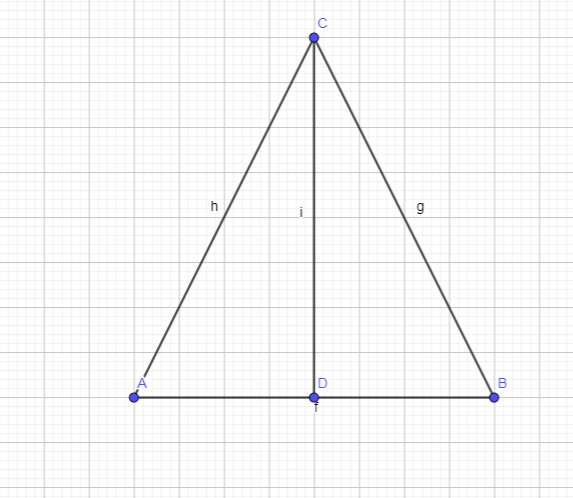
Այստեղ եռանկյան կիսորդը CM ուղիղն է հետեւաբար AC=BC:
C անկյունը գտնվում է եռանկյան գագաթին։ Հետեւաբար C-ն ամենաբարձր անկյունն է այս եռանկյան մեջ:


AC = CB
ACE = BCF(հանդիպակաց) => AEC = FCB => BF = AE