1. Պարզի՛ր, թե քերականական ո՛ր հատկանիշի  հիման վրա է կազմվել
 յուրաքանչյուր խումբը (խմբի բոլոր բաոերն ի՞նչ ընդհանուր հատկանիշ 
ունեն):

Ա. Ուրարտու, Արա Գեղեցիկ, Արագած, Արգիշտի, Նեղոս, Վահան Տերյան, «Անուշ», Ռուսաստանի Դաշնություն:-Հատուկ անուններ։
Բ. Մանկություն, միամտություն, ուրախություն, սուգ, վիշտ, ահ, 
հնարավորություն:-Ոչ շոշափելի։
Գ. Հայր, մայր, մարդ, կին, ընկեր, եղբայր, հոգեբան, ուսանողուհի,
 դերասանուհի, անձնավորություն:-Անձ։

2․Դո՛ւրս գրիր գոյականները՝ նշելով տեսակը, թիվը, հոլովը, առումը։

Աշուն

Աշնան օրերն են հասել,

Իջել է ամպը սարին,

Եւ հրաժեշտ է ասել,

Կռունկը մեր աշխարհին:

Բարդին էլ չի սոսափում

Արագիլի թեւի տակ,

Դեղին թերթեր է թափում

Առվակի մեջ կապուտակ:

Կարմիր խարույկ է կարծես

Ծեր տանձենին անտառի,

Թվում է, թե մոտ վազես,

Ձեռք ու ոտքդ կվառի…

Քամին շատ էր թափառել,

Պարապ-սարապ թեւը կախ,

Բայց արդեն գործ է ճարել,

Տեսեք ինչքան է ուրախ:

ամպ-հասարակ գոյական, եզակի թիվ, ուղղական հոլով ,որոշյալ առում
Կռունկը-հասարակ գոյական, եզակի թիվ, ուղղական հոլով ,որոշյալ առում
աշխարհ-հասարակ գոյական, եզակի թիվ, տրական հոլով
աշնան-հասարակ գոյական, եզակի թիվ, սեռական հոլով
բարդի-հասարակ գոյական, եզակի թիվ, ուղղական հոլով ,որոշյալ առում
սարին-հասարակ գոյական, եզակի թիվ, տրական հոլով
արագիլին-հասարակ գոյական, եզակի թիվ, սեռական հոլով
փերի-հասարակ գոյական, եզակի թիվ, սեռական հոլով

Համո Սահյան

3․ Հետևյալ թվականները տառերով գրի՛ր․

654-Վեց հարյուր հիթսունչորս

659-Վեց հարյուր հիթսունինը

5478-հինգ հազար չորս հարյուր յոթանասունութ

3546-երեք հազար հինգ հարյուր քառասունվեց

12893-տասերկու հազար ութ հարյուր ինսուներեք

75648-յոթանասունհինգ հազար վեց հարյուր քառասունութ

489523-չորս հարյուր ութսունինը հազար հինգ հարյուր քսաներեք

146782-հարյուր քառասունվեց հազար յոթ հարյուր ութսուներկու

4․ Ստեղծագործական աշխատանք՝ ազատ թեմայով։

1․ Կրճատիր կոոտորակը․

1.9/18=1/2

2.8/10=4/5

3.6/8=3/4

4.5/20=1/4

5.18/24=9/12

6.6/9=2/3

8.4/16=2/8

9.18/36=9/18

10.6/42=3/21

11.13/39=13/3

12.21/28=3/4

13.63/77=9/11

15.21/63=1/3

16.30/84=15/42

17.50/125=10/25

18.72/108=46/54

19.49/112=7/16

20.240/320=3/4

2. Պարզեցրո՛ւ արտահայտությունը.

1. 3x+27
2. -48x+24
3. 4x+3
4. -2-7x²
5. 5+10x²
6. 15x²+6x
7. -7x² +8x
8. 2x²-3x
9. -26x+12
10. 90x-48
11. -18x-59
12. 2x²+(-8x)
13. -2x+2
14. 14-5x
15. 34x+19
16. -38x+24

3. Կատարի՛ր գումարում.

1)1/3+2/3=(1+2)/3=3/3
2)1/2+1/3=(3+2)/6=5/6
3)2/5+1/2=(4+5)/10=9/10
4)3/7+2/3=(9+14)/21=23/21
5)3/4+2/5=(15+8)/20=23/20
6)3/5+1/5=(3+1)/5=4/5
7)5/9+1/2=(10+9)/18=19/18
8)3/5+3/8=(24+15)/40=39/40
9)5/9+3/7=(35+27)/63=62/63
10)5/11+1/4=(20+11)/44=31/44
11)3/7+1/6=(18+7)/42=25/42
12)3/14+3/4=(12+42)/56=54/56

4. Հաշվի՛ր տարբերությունը.

13)1/2-1/3=(3-2)/6=1/6
14)4/5-2/3=(12-10)/15=2/15
15)2/3-1/6=(4-1)/6=3/6=1/2
16)3/5-1/2=(6-5)/10=1/10
17)8/9-2/5=(40-18)/45=22/45
18)4/7-1/9=(36-7)/63=29/63
19)2/5-1/4=(8-5)/20=3/20
20)5/8-2/6=(30-16)/48=14/30
21)4/15-1/10=(8-3)/30=5/30
22)7/20-1/5=(7-4)/20=3/20
23)3/18-1/12=(6-3)/36=3/36=1/12
24)9/24-3/16=(18-9)/48=9/48=3/16

Կրկնել նախորդ թեմանները։

Կարգի բերել բլոգները։Պատրաստ լինել  բանավոր հարցմանը։

Ծանոթանալ,սովորել․

Թեման.Մեխանիկական շարժում:Շարժմանհարաբերականություն:Նյութական կետ:Շարժման հետագիծ:Ճանապարհ:

Պատասխանել հետևյալ  հարցերին..

1.Ինչն են անվանում մեխանիկական շարժում։Մեխանիկիական շարժում են կոչվում ժամանկի ընթացքում մարմնի դիրքի փոփոխությունը այլ մարմինների նկատմամբ։

2.բերել մեխանիկական շարժման օրինակներ։Մեխանիկական շարժման օրինակներ են՝ գնդակի գլորվելը, մեքենայի գնալը, մարդու քայլելը և այլն:

3.որ մարմինն են անվանում հաշվարկման մարմին։Հաշվարկման մարմին կոչվում է այն մարմինը, որի նկատմամբ դիտարկում են այլ մարմինների դիրքերը։

4.Ինչն են անվանում նյութական կետ։Այն մարմինը, որի չափերը տվյալ պայմաններում կարելի է անտեսել, կոչվում է նյութական կետ:

5.Որ դեպքում մարմինը կարելի է համարել նյութական կետ,.որ դեպքում՝ոչ։

Այն մարմինը, որի չափերը տվյալ պայմաններում կարելի է անտեսել, կոչվում է նյութական կետ։

8.Ինչով է տարբերվում հետագիծն անցած ճանապարհից:

Մարմնի հետագիծը այն գիծն է, որով շարժվել է մարմինը, իսկ մարմնի անցած ճանապարհը որոշակի ժամանակամիջոցում անցած հետագծի երկարությունն է:

Սովորել․Է․Ղազարյանի դասագրքից՝(Ֆիզիկա 7) էջ21-ից,մինչև էջ 28-ը։

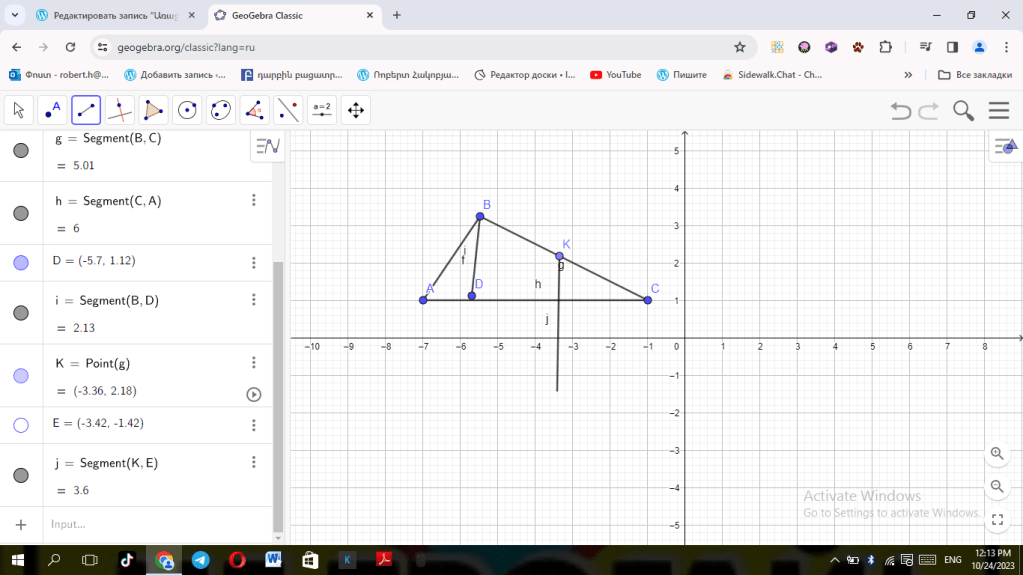
Եռանկյունը բազմանկյուն է, որն ունի երեք կողմ։ Այլ կերպ այն կարելի է սահմանել որպես այնպիսի պատկեր, որը կազմված է միևնույն ուղղի վրա չգտնվող երեք կետերից, և այդ կետերը զույգ առ զույգ միացնող երեք հատվածներից։ Այդ կետերը կոչվում են եռանկյան գագաթներ, իսկ հատվածները՝ նրա կողմեր։ 

A, B, և C գագաթներով եռանկյունը հաճախ նշանակում են ΔABC: Այդ նույն եռանկյունը կարելի է նշել նաև այլ կերպ. օրինակ՝  ΔBAC, ΔCAB

Երեք անկյունները՝ <BAC-ն, <ABC-ն և <ACB-ն կոչվում են եռանկյան անկյուններ: Անկյունները նշանակվում են նաև մեկ տառով՝ <A, <B և <C:

Եռանկյան բոլոր կողմերի երկարությունների գումարը կոչվում է նրա պարագիծ:

Երկու պատկերներ, այդ թվում նաև երկու եռանկյուններ կոչվում են հավասար, եթե վերադրումով դրանք կարող են համընկնել:

Հավասար եռանկյունների մեջ համապատասխանաբար հավասար (այսինքն՝ վերադրելիս համընկնող) կողմերի դիմաց ընկած են հավասար անկյուներ, և ընդհակառակը՝ համապատասխանաբար հավասար անկյունների դիմաց ընկած են հավասար կողմեր:

ABC և A₁B₁C₁ եռանկյունների հավասարությունը նշանակվում է այսպես՝ ΔABC= ΔA₁B₁C₁

Առաջադրանքներ

1)ABC եռանկյան կողմը հավասար է 17սմ և հայտնի է որ բոլոր կողմերկ երկարությունները ամբողջ թվեր են։ Գտնել եռանկյան պարագիծը եթե AC կողմը կրկնակի մեծ է AB կողմից, իսկ BC կողմը 10սմ-ով փոքր է AC կողմից:        

AC=34
BC=24
BA=17
P=75                                                                     

2)Եռանկյան պարագիծը 48սմ է, իսկ կողմերից մեկը՝ 18սմ: Գտեք մյուս երկու կողմերը, եթե նրանց տարբերությունը 4,6սմ է:       

BA=18
AC=12,7
BC=17,3
P=48

3) ABC եռանկյան պարագիծը 15 սմ է: BC կողմը AB կողմից մեծ է 2սմ-ով, իսկ AB կողմը AC կողմից փոքր է 1սմ-ով: Գտեք եռանկյան կողմերը:
BC=6սմ
AC=5սմ
BA=4սմ

Լրացուցիչ

4) Եռանկյան կողմերի երկարությունները հարաբերում են ինչպես 5:12:13, իսկ փոքր կողմը 10 սմ է: Գտնել եռանկյան պարագիծը:

5) Եռանկյան մի կողմը 10 սմ է,մյուսը` երկու անգամ մեծ այդ կողմից, երրորդը՝ 5սմ-ով փոքր է երկրորդ կողմից: Գտնել եռանկյան պարագիծը:

6) Եռանկյան մի կողմը հավասար է 12 սմ, մյուս երկու կողմերի տարբերությունը 4սմ է, իսկ պարագիծը՝ 32սմ է: Գտնել եռանկյան կողմերը:

Եռանկյունը բազմանկյուն է, որն ունի երեք կողմ։ Այլ կերպ այն կարելի է սահմանել որպես այնպիսի պատկեր, որը կազմված է միևնույն ուղղի վրա չգտնվող երեք կետերից, և այդ կետերը զույգ առ զույգ միացնող երեք հատվածներից։ Այդ կետերը կոչվում են եռանկյան գագաթներ, իսկ հատվածները՝ նրա կողմեր։ 

A, B, և C գագաթներով եռանկյունը հաճախ նշանակում են ΔABC: Այդ նույն եռանկյունը կարելի է նշել նաև այլ կերպ. օրինակ՝  ΔBAC, ΔCAB

Երեք անկյունները՝ <BAC-ն, <ABC-ն և <ACB-ն կոչվում են եռանկյան անկյուններ: Անկյունները նշանակվում են նաև մեկ տառով՝ <A, <B և <C:

Եռանկյան բոլոր կողմերի երկարությունների գումարը կոչվում է նրա պարագիծ:

Երկու պատկերներ, այդ թվում նաև երկու եռանկյուններ կոչվում են հավասար, եթե վերադրումով դրանք կարող են համընկնել:

Հավասար եռանկյունների մեջ համապատասխանաբար հավասար (այսինքն՝ վերադրելիս համընկնող) կողմերի դիմաց ընկած են հավասար անկյուներ, և ընդհակառակը՝ համապատասխանաբար հավասար անկյունների դիմաց ընկած են հավասար կողմեր:

ABC և A₁B₁C₁ եռանկյունների հավասարությունը նշանակվում է այսպես՝ ΔABC= ΔA₁B₁C₁

Առաջադրանքներ

1)ABC եռանկյան կողմը հավասար է 17սմ և հայտնի է որ բոլոր կողմերկ երկարությունները ամբողջ թվեր են։ Գտնել եռանկյան պարագիծը եթե AC կողմը կրկնակի մեծ է AB կողմից, իսկ BC կողմը 10սմ-ով փոքր է AC կողմից:                                                                             

2)Եռանկյան պարագիծը 48սմ է, իսկ կողմերից մեկը՝ 18սմ: Գտեք մյուս երկու կողմերը, եթե նրանց տարբերությունը 4,6սմ է:       

3) ABC եռանկյան պարագիծը 15 սմ է: BC կողմը AB կողմից մեծ է 2սմ-ով, իսկ AB կողմը AC կողմից փոքր է 1սմ-ով: Գտեք եռանկյան կողմերը:

Լրացուցիչ

4) Եռանկյան կողմերի երկարությունները հարաբերում են ինչպես 5:12:13, իսկ փոքր կողմը 10 սմ է: Գտնել եռանկյան պարագիծը:

5) Եռանկյան մի կողմը 10 սմ է,մյուսը` երկու անգամ մեծ այդ կողմից, երրորդը՝ 5սմ-ով փոքր է երկրորդ կողմից: Գտնել եռանկյան պարագիծը:

6) Եռանկյան մի կողմը հավասար է 12 սմ, մյուս երկու կողմերի տարբերությունը 4սմ է, իսկ պարագիծը՝ 32սմ է: Գտնել եռանկյան կողմերը:

46.Պատասխան՝90:2=45

47.Այո

48.Այո

49.Ոչ

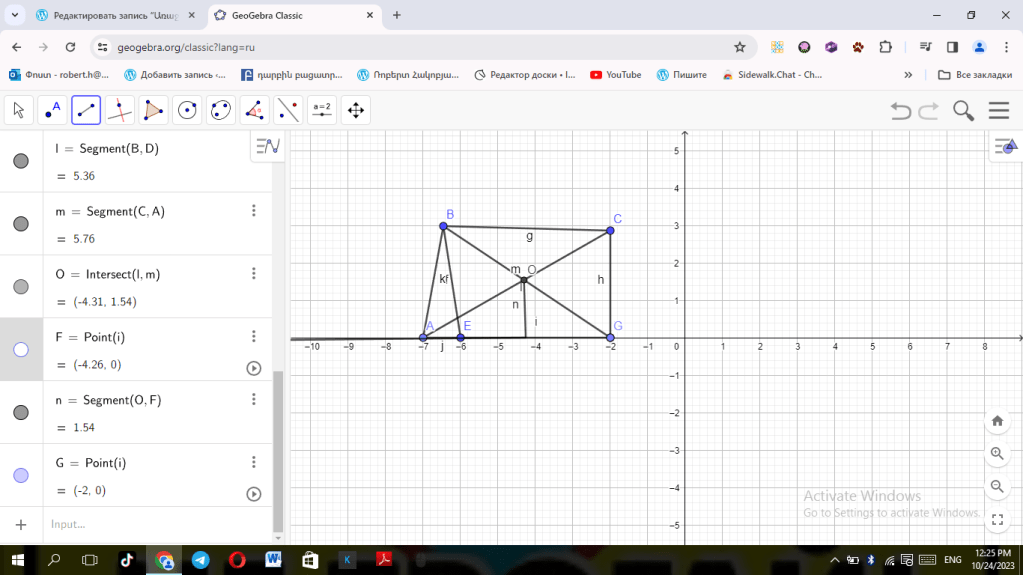
Հավելյալ խնդիրներ

1) OE Ճառագայթը AOB անկյունը տրոհում է երկու անկյան: Գտեք <AOB-ն, եթե <AOE=56⁰, <EOB=123⁰34’ <AOB=56⁰+123⁰34=179⁰34

2) Ուղղանկյունաձև այգու հողամասի երկարությունը  5մ է, իսկ լայնությունը`  6մ: Գտեք այդ հողամասի պարագիծը:=22մ

3.Հակադիր անկյունները-ABC-DBE-ABD-CBE Փռված անկյուններ-ABE-DBC

4.ABM-CBN

5.Պատասխան՝110:2=55

6) Ուղղանկյունաձև այգու հողամասի երկարությունը  6մ է, իսկ լայնությունը`  7մ: Գտեք այդ հողամասի պարագիծը=26մ

7)  OE Ճառագայթը AOB անկյունը տրոհում է երկու անկյան: Գտեք <AOB-ն, եթե <AOE=56⁰, <EOB=12⁰3’: <AOB=<AOE+<EOB=68⁰3

8) Քառակուսաձև այգու հողամասի երկարությունը  6մ է: Գտեք այդ հողամասի պարագիծը:=24մ

9)  OE Ճառագայթը AOB անկյունը տրոհում է երկու անկյան: Գտեք <AOB-ն, եթե <AOE=21⁰, <EOB=123⁰31’: <AOB=<AOE+<EOB=144⁰31

10)  OE Ճառագայթը AOB անկյունը տրոհում է երկու անկյան: Գտեք <AOB-ն, եթե <AOE=50⁰, <EOB=12⁰34’: <AOB=<AOE+<EOB=62⁰34

Առաջադրանքներ

34. ոչ նրանք գնվում են մի ուղղի վրա

35. 180 փռված անկյուն

36.180 — 43=137

37.180-30=150:2=75,75+30=105

38. 180+40=220:2=110,110-40=70

39.180:4=45 ,45×3=135

40. 180:6=30, 30×5=150

41.180-36=144

42. BCH, CHN, CNM, MCL, LCK,KCB, 12ակյուն