Հարցեր և առաջադրանքներ

1․Ո՞ր բազմանկյունն է կոչվում կանոնավոր:
Կանոնավոր բազմանկյուն է կոչվում այն ուռուցիկ բազմանկյունը, որի բոլոր անկյունները  և բոլոր կողմերը հավասար են։

2.Գրել կանոնավոր բազմանկյան անկյան հաշվման բանաձևը:

3. GEOGEBRA ծրագրով գծել կանոնավոր բազմանկյուններ:

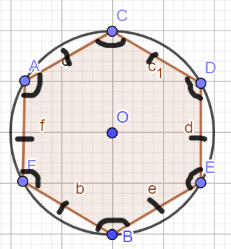
4. Գծագրից գտնել ուռուցիկ բազմանկյունները և նշել նրանց համարները:

1,5,6,9,10

5. Գտնել կանոնավոր n-անկյան անկյունները, եթե՝
ա) n=3 α₃=3-2։3*180=60
բ) n=5 α₅=5-2։5*180=108
գ) n=6 α₆=6-2։6*180=120
դ) n=10 α₁₀=10-2։10*180=144
ե) n=18 α₁₈=18-2։18*180=160

6. Որոշել կանոնավոր 15 -անկյան ներքին և արտաքին անկյունները:

7. Քանի՞ կողմ ունի կանոնավոր բազմանկյունը, եթե նրա յուրաքանչյուր անկյունը հավասար է`  
ա) 150^o
(n-2)/n*180=150
(n-2)/n=5/6
n-2=5/6n
n/6=2
n=12  
բ) 135^o
(n-2)/n*180=135
(n-2)/n=3/4
n-2=3/4n
n/4=2
n=8
գ) 90^o
(n-2)/n*180=90
(n-2)/n=1/2
n-2=1/2n
n/2=2
n=4
դ) 60^o
(n-2)/n*180=60
(n-2)/n=1/3
n-2=1/3n
n/3=2
n=6   
ե)30^o
(n-2)/n*180=30
(n-2)/n=
n-2=
n/=2
n=12

8. Քանի՞ կողմ ունի կանոնավոր բազմանկյունը, եթե նրա արտաքին անկյուններից յուրաքանչյուրը հավասար է՝ 
ա) 40^o   
180-40=140
(n-2)/n*180=140
(n-2)/n=7/9
n-7/9n=2
2/9n=2
n=9
բ) 36^o
180-36=144
(n-2)/n*18=144/180
n-2=4/5n
4/5n=2
n=10   
գ) 30^o
180-30=150
(n-2)/n*180=150
(n-2)/n=5/6
n-2=5/6n
n/6=2
n=12   
դ) 24^o
180-24=156
(n-2)/n*180=156
(n-2)/n=13/15
n-2=13/15n
2/15n=2
n=15

9. Որոշել կանոնավոր բազմանկյան կողմերի թիվը կամ եզրակացրու, որ այդպիսի բազմանկյուն գոյություն չունի, եթե տրված է բոլոր ներքին անկյունների գումարը:

ա) Եթե անկյունների գումարը 2050 աստիճան է, ապա բազմանկյունը գոյություն ….., կողմերի թիվը` …..:

բ) Եթե անկյունների գումարը 1980 աստիճան է, ապա բազմանկյունը գոյություն ……, կողմերի թիվը` …..:

1. Որքա՞ն է թթվածնի վալենտականությունը և օքսիդացման աստիճանը թթվածնի պարզ նյությում:
2. Ի՞նչ կապեր են առկա թթվածին պարզ նյութի մոլեկուլում:
3. Գազային խառնուրդը պարունակում է 2,5 մոլ թթվածին և 3 մոլ օզոն:Ո՞րքան է խառնուրդի զանգվածը(գ)
4. Ի՞նչ ծավալ են զբաղեցնում 5 մոլ հելիումը և 0,5 մոլ արգոնը:
5. Որքա՞ն է 67,2 ծավալով ազոտի (II)քսիդի (NO) զանգվածը:
6. Գրե՛լ Al, Sc,Ge,Nb,Mo,Tc ,Xe տարրերի էլեկտրոնային բանաձևերը:
7. Ո՞րքան է նյութի մոլային զանգվածը, եթե նրա 10 գրամը 0,25 մոլ է:
8. Որքա՞ն է 106,5 գ զանգվածով ֆոսֆորի (V) օքսիդի (P₂O₅) նյութաքանակը:
9. Որքա՞ն է 2 մոլ երկաթի (II) սուլֆիդի (FeS ) զանգվածը:
10. Լրացրե ́ք բաց թողնված քիմիական նշան­ները.
    ա)Ar(…) = 11
    գ)Ar(… ) = 28
    բ)Ar(… ) = 108
11. Լրացրե ́ք բաց թողնված քիմիական նշան­ները.
    ա)Ar(…) = 55 գ)Ar(… ) = 64
    բ)Ar(… ) = 14 դ)Ar(… ) = 39

Հարցեր և առաջադրանքներ։

1․Ինչպիսի՞ հնարավոր դասավորվածություն կարող են ունենալ տրված շրջանագծերը եթե նրանց կենտրոնների միջև հեռավորությունը հավասար է 20սմ, իսկ շառավիղները համապատասխանաբար հավասար են՝
ա) 15 սմ և 10 սմ բ) 10 սմ և 10 սմ գ) 5սմ և 7 սմ: GEOGEBRA ծրագրով գծել ստացված պատկերները։

2.Հարթության վրա երկու իրարից տարբեր շրջանագծեր կարող են (ընտրիր ճիշտ պատասխանները)՝ 

• չհատվել
• չունենալ ընդհանուր կետ
• հատվել երեք կետերում
• ունենալ 6 ընդհանուր կետ

3․Քանի՞ ընդհանուր կետ ունեն շրջանագծերը: Ընտրել ճիշտ տարբերակը:

• 2
• անվերջ թվով
• 1
• 0

4․Գտնել ED-ն, եթե AC= 4 սմ, իսկ շրջանագծերի կենտրոնների միջև հեռավորությունը 5 սմ է: 

ED=AD-AE=1

5․Գծել տրված O և B կենտրոններով մեկ ընդհանուր կետ ունեցող շրջանագծեր, որոնց շառավիղները հավասար են՝ r₁=28 սմ և r₂=10 սմ: Հաշվել OB հեռավորությունը:

38

6․ Տրված են այս երկու շրջանագծերը, որոնք ունեն մեկ ընդհանուր կետ:

r₁-ը և r₂-ը համապատասխանաբար մեծ և փոքր շրջանագծերի շառավիղներն են: Ընտրել ճիշտ պնդումը:

• OB>r₁+r₂
• r₁+r₂=OB
• r₁+r₂>OB

Հարցեր և առաջադրանքներ:

1․Պատկանու՞մ է արդյոք -1 թիվը թվային բազմությանը (գրառումը կատարեք ∈ և ∉ նշանների օգնությամբ):

ա)[-4;0] ∈
բ)(-2;4) ∈
գ)(-∞;-2] ∈
դ)(-3;+∞) ∈
ե)N ∉
զ)Z ∈
է)Q ∈
ը)R ∈

2․ Արդյո՞ք ճիշտ է հետևյալ պնդումը՝ −1.67∉(−∞;−5)

ա) ոչ
բ) այո

3․ Կոորդինատային առանցքի վրա նշել
ա) [2;5] հատվածը
բ) (2;5) միջակայքը

4․Պատկերեք նշված բազմությունները թվային ուղղի վրա՝

ա) [4;9]
բ) (-2;7]
գ)[-1;9)
դ) (0;8)

5․ Կոորդինատային առանցքի վրա պատկերել թվային միջակայքերը․

ա) [-2;3] և [0;2] [0;2]
բ) [-4;6] և [-1;5] [-1;5]
գ) [-5;2] և [3;5] հատման կետեր չունեն
Նրանք ընդհանուր կետեր ունե՞ն։ Եթե այո, գրառել այդ բազմությունների ընդհանուր մասը (հատումը):

Հարցեր և առաջադրանքներ։

1․ Ո՞ր  շրջանագիծն  է  կոչվում  բազմանկյանը  արտագծյալ:
Եթե բազմանկյան բոլոր գագաթները գտնվում են շրջանագծի վրա, ապա շրջանագիծը կոչվում է այդ բազմանկյան արտագծյալ շրջանագիծ:  

2․ Քանի՞  շրջանագիծ  կարելի  է  արտագծել  տրված  եռանկյանը:
1

3․ Հնարավո՞ր  է  արդյոք  ցանկացած  քառանկյան  արտագծել  շրջանագիծ: 
ոչ

4․ Ի՞նչ  հատկություն  ունի  շրջանագծին  ներգծված  քառանկյունը:
Ցանկացած ներգծյալ քառանկյուն հանդիպակաց անկյունների գումարը 180⁰ է:

5․Սեղանին արտագծված է շրջանագիծ: Հաշվիր սեղանի մյուս անկյունները, եթե անկյուններից մեկը՝ F=10° է:

Ցանկացած ներգծյալ քառանկյան հանդիպակաց անկյունների գումարը 180⁰ է:
E+F=180 ապա E=170
Ցանկացած սեղանի սրունքին առընթեր անկյունների գումարը 180° է:
Քանի որ E=10 ապա G=170

6․ Գտնել B և D անկյունները։

Ցանկացած ներգծյալ քառանկյան հանդիպակաց անկյունների գումարը 180⁰ է:
Քանի որ R=85 ապա D=95
Քանի որ I=117 ապա B=63

7․ O կենտրոնով շրջանագծին ներգծված է ZXY եռանկյունն այնպես, որ ZX-ը  տրամագիծ է։ ZY աղեղի աստիճանային չափը հավասար է 104⁰ -ի։ Գտնել ZXY եռանկյան անկյունները։

Կիսաշրջանագծի վրա հենված ներգծյալ անկյունը 90° է դրանից => Y=90^o
Ներգծյալ անկյունը չափվում է այն աղեղի կեսով, որի վրա նա հենվում է՝ =>
x=ZY/2=52 Z=180-90-52=38

8․ Օգտվելով գծագրից, գտնել ∠ B-ը։

Կիսաշրջանագծի վրա հենված ներգծյալ անկյունը 90° է դրանից => C=90^o
B=180-90-46=44

9․ Գտնել ∠ R-ը և ∠B-ն։

Ցանկացած ներգծյալ քառանկյան հանդիպակաց անկյունների գումարը 180⁰ է:
Քանի որ A=92 ապա R=88
Քանի որ E=74 ապա B=106

10․ ABC եռանկյանը արտագծված է շրջանագիծ։ Գտնել այդ շրջանագծի շառավիղը, եթե AC=24 սմ, ∠A=60⁰, ∠B=30⁰:
r=AB/2 քանի որ ∠B=30 է , եռանկյուն ABC ուղղանկյուն եռանկյուն է => AC=AB/2 => r=6

11. Արդյոք կարելի՞ է տրված ABCD քառանկյանը արտագծել շրջանագիծ, եթե
ա)∠A=64⁰, ∠ B=95⁰, ∠C=106⁰
բ) ∠A=72⁰, ∠B=69⁰, ∠D=111⁰
գ) ∠A=90⁰, ∠C=90⁰, ∠D=80⁰:

Հարցեր և առաջադրանքներ:

1. Ո՞ր թվեր են պատկանում տրված միջակայքին՝ (−∞;−5)

ա) -6 այո
բ) 1 ոչ
գ) 5 ոչ
դ) -1 ոչ
ե) 20 ոչ
զ) 10 ոչ
է) -10 այո
թ) -9 այո

2. Պարզել՝ ճիշտ է, թե սխալ հետևյալ պնդումը՝ −12∈(−12;7]

ա)սխալ է
բ)ճիշտ է

3. Ո՞ր թվեր են պատկանում տրված հատվածին՝  [−12;0]

ա) −9
բ) −10
գ) 20
դ) −6
ե) −1
զ) 10
է)1
թ)5

4. Ո՞ր թվերը չեն պատկանում այս միջակայքին՝ (−1;10)

ա) 12
բ) 1
գ) 10
դ) −1
ե) 5
զ) 2

5. Ընտրիր x∈(−∞;−1] միջակայքի պատկերը թվային առանցքի վրա, եթե a=−1

• 
• 
• 
• 
  Պատասխան՝

6.Գրառել նշանակումը՝

ա)[2;4]
բ)(2;4)
գ)(2;4]
դ)[2;4)
ե)(5;+∞)
զ)[5;+∞)
է)(-∞;0)
ը)(-∞;0]

7. Կարդալ թվային բազմության անվանումը և այն պատկերել այն կոորդինատային ուղղի վրա՝

8․ Թվարկել թվային բազմությանը պատկանող բոլոր ամբողջ թվերը․

ա)-3,-2,-1,0,1
բ)-2,-1,0
գ)-3,-2,-1,0
դ)-2,-1,0,1
ե)-2,-1,0,1,2,3
զ)-1,0,1,2
է)-2,-1,0,1,2
ը)-1,0,1,2,3

9․ Կոորդինատային առանցքի վրա նշել այն թվերը, որոնք՝

10․Անվանել թվային բազմությանը պատկանող չորս ամբողջ թվեր՝

ա)0,1,2,3…..
բ)1,2,3,4…..
գ)…0
դ)…0,1

11․Գրառել նկարում պատկերված բազմությունները՝

ա)[3;7]
բ)(3;7)
գ)(5;6]
դ)[5;6)
ե)[7;+∞)
զ)(-∞;8)
է)(7;+∞)
ը)(-∞;8]

Հարցեր և առաջադրանքներ։

1․ Գրել անկյան կիսորդի հատկությունը։
Անկյան կիսորդի ցանկացած կետ հավասարահեռ է անկյան կողմերից:

2․ Թվարկել եռանկյան նշանավոր կետերը։

3․ Եռանկյան մեջ տարված են միջնագծեր և բարձրություններ: Դրանց վերաբերյալ թվարկված պնդումներից որ՞ն է ճիշտ:

ա Եռանկյան բարձրությունները հատվելիս բաժանվում են 4:1 հարաբերությամբ հատվածների:

բ Եռանկյան միջնագծերը հատվելիս բաժանվում են 2:1 հարաբերությամբ հատվածների:

գ Եռանկյան միջնագծերը հատման կետով բաժանվում են 3:2 հարաբերությամբ հատվածների:

դ Բոլոր պնդումներն էլ սխալ են:

4․ Ո՞ր  շրջանագիծն  է  կոչվում  բազմանկյանը  ներգծյալ։
Բազմանկյան ներգծյալ կոչվում է այն շրջանագիծը, որը անցնում է բոլոր բազմանկյանի անկյուններից։ Դա այն շրջանագիծն է, որը անցնում է բոլոր անկյունների միջոցով։

5․ Նշել եռանկյունները, որոնց արտագծված է շրջանագիծ:

ա) PRT բ) EFG գ) KLM դ) MNL ե) ABC զ) DEF

6․ ABC հավասարասրուն եռանկյան AB և BC կողմերին տարված բարձրությունները հատվում են M կետում: BM ուղիղը AC հիմքը հատում է N կետում: Որոշիր NC, եթե AC=36սմ

7․ Հաշվել քառանկյան անհայտ կողմը, եթե նրան ներգծված է շրջանագիծ: FG=10սմ, EH=15սմ, HG=12սմ

Հարցեր և առաջադրանքներ

1․ Ո՞ր  շրջանագիծն  է  կոչվում  բազմանկյանը  ներգծյալ։
Եթե բազմանկյան բոլոր կողմերը շոշափում են շրջանագիծը, ապա շրջանագիծը կոչվում է այդ բազմանկյան ներգծյալ շրջանագիծ:

2․ Քանի՞  շրջանագիծ  կարելի  է  ներգծել  տրված  եռանկյանը:

1

3․GEOGEBRA ծրագրով գծիր եռանկյուն, ներգծիր եռանկյանը շրջանագիծ, նկարը ցույց տուր։

4․Շրջանագծին արտագծած հավասարասրուն սեղանի հիմքերը հավասար են 4 սմ և 9 սմ։ Գտնել սեղանի պարագիծը։
2x=4+9
x=6,5

5․Ներգծյալ շրջանագծի շոշափման կետում հավասարասրուն եռանկյան սրունքը տրոհվում է 3 սմ և 4 սմ երկարությամբ հատվածների՝ հաշված հիմքից: Գտե՛ք այդ եռանկյան պարագիծը:

6․ Գտե՛ք 6 սմ և 8 սմ էջերով և 10սմ ներքնաձիգով ուղղանկյուն եռանկյանը ներգծած շրջանագծի շառավիղը:
r=a+b-c/2
r=6+8-10/2=2

7․ Ուղղանկյուն եռանկյան ներքնաձիգը 13սմ է, իսկ էջերի գումարը՝ 17սմ: Գտե՛ք եռանկյան ներգծյալ շրջանագծի շառավիղը:

r=a+b-c/2
r=17-13/2=2

8․ Ուղղանկյուն եռանկյան ներքնաձիգը 15 սմ է, իսկ պարագիծը՝ 36սմ: Գտե՛ք այդ եռանկյան ներգծյալ շրջանագծի շառավիղը:

a+b+15=36
36-15=21
a+b=21
r=a+b-c/2
r=21-15/2=3

1.Ընդարձակի´ր նախադասությունները՝ օգտագործելով վերաբերականներ։

• Վախենո՞ւմ ես:
• Հիշեցնե՞մ:
• Պիտի համոզե՞մ:
• Ծաղկե՞լ է:
• Կտանե՞ս:
• Պիտի կարողանա´ս:
• Օգնի´ր:
• Հիշի´ր:
• Վստահի´ր:
• Բերե´ք:

1. Գրի՛ր շարադրություն հետևյալ թեմաներից մեկով․

• Գարունը մոտենում է
• Խոհեր կյանքի մասին
• Իմ երևակայական աշխարհը
• Իմ ազատ ժամանակը
• Համակարգչային խաղերի օգուտն ու վնասը
• Ես հավատում եմ, որ
• Աշխարհը իմ պատուհանից
• Արդար չեմ համարում, որ․․․
• Այլ թեմա

Երբ ես, իմ անելիքները դպրոցում վերջացնում եմ, գնում եմ տուն։Տանը մի քիչ հեռախոսով եմ զբաղվում և գնում եմ դուրս ընկերներիս հետ խաղալու։Ես և իմ ընկերները շատ ենք սիրում ֆուտբոլ խաղալ և ամբողջ օրը ֆուտբոլի դաշտում ֆուտբոլ ենք խաղում։Երբ գիշերը իմ բոլոր ընկերները գնում են տուն, ես էլ եմ տուն գնում։Տանը մայրիկիս պատրաստած ուտելիքն եմ ուտում և գնում եմ իմ սենյակ քնելու։

Առաջադրանքներ։

1․Գումարել թվային անհավասարությունները։

ա) 18>11 և 15>7 18+15>11+7, 33>18
բ) -4>-6 և 13>8 -4+13>-6+8, 9>2
գ) -16<-7 և 12<37 -16+12<-7+37, 4<30
դ) -9<0 և 5<19 -9+5<0+19, -4<19

2. Գումարել թվային անհավասարությունները։

ա)14>11 և 10>9 14+10>11+9, 24>20
բ)-2>-3 և 3>2 -2+3>-3+2, 1>-1
գ)-6<-5 և 2<3 -6+2<-5+3, -4<-2
դ)-8<=0 և 8<=9 -8+8<=0+9, 0<=1

3․Բազմապատկել թվային արտահայտությունները։

ա)14>10 և 2>1 14*2>10*1, 28>10
բ)5>3 և 6>5 5*6>3*5, 30>15
գ)6<7 և 2<3 6*2<7*3, 12<21
դ)8<9 և 1<2 8*1<9*2, 8<18

4․Գումարել  անհավասարությունները:
ա) 22>17 և 3,2>0,6 22+3,2>17+0,6, 25,2>17,6
բ) 53<65 և 7,6<10,9 53+7,6<65,10,9, 60,6<75,9

5․Զբոսաշրջիկ առաջին օրն անցավ 20 կմ-ից ավելի, իսկ երկրորդ օրը 25 կմ-ից ավելի։ Արդյո՞ք կարելի պնդել, որ զբոսաշրջիկն անցել է 45 կմ-ից ավելի ճանապարհ։ Պատասխանը հիմնավորել։
1 օր+2 օր>45

6․ Ուղղանկյան երկարությունը 13 սմ-ից փոքր է, իսկ լայնությունը՝ 5 սմ-ից փոքր։Արդյո՞ք կարելի պնդել, որ ուղղանկյան մակերեսը 65 սմ²-ից ավելի է։ Պատասխանը հիմնավորել։
>13+>5>65