1. Հաշվել  RNK անկյունը և շրջանագծի շառավիղը, եթե MN=10 սմ է և ∠ RON=30°

<RNO=180-30-90=60
<ONK=90
<RNK=60+90=150

2. Հաշվել շրջանագծի շառավիղը, եթե AO=9սմ  է և ∠ OAK=30°

3. Շրջանագծի A կետով տարված են շոշափող և շառավիղին հավասար լար։ Գտեք լարի և շոշափողի կազմած անկյունը։ GEOGEBRA ծրագրով գծել գծագիրը:

4. Շրջանագծի շառավիղին հավասար KM լարի ծայրակետերով տարված են այդ շրջանագծի շոշափողներ, որոնք հատվում են N կետում։ Գտեք KMN եռանկյան անկյունները։ GEOGEBRA ծրագրով գծել գծագիրը:

5. Շրջանագծին A, C և E կետերում տարված են AB, BD և DE շոշափողները, իսկ AB=7 սմ: Որոշիր ACE եռանկյան պարագիծը:

P=14+14+14=42

Հարցեր և առաջադրանքներ։

1․ Ո՞ր ուղիղն է կոչվում շոշափող:
Եթե շրջանագծի կենտրոնի հեռավորությունն ուղղից հավասար է շրջանագծի շառավղին, ապա շրջանագիծն ու ուղիղը ունեն մեկ ընդհանուր կետ այդ դեպքում ուղիղն անվանում են շրջանագծի շոշափող:

2. Գրել շրջանագծի շոշափողի հատկությունները:
Եթե միևնույն կետից շրջանագծին տարված են երկու շոշափողներ, ապա

ա) շոշափման կետերի հեռավորությունները տրված կետից հավասար են,

բ) շրջանագծի կենտրոնով և տրված կետով անցնող ուղիղը կիսում է շոշափողների կազմած անկյունը:

3. Տրված է՝  ∠CAO=29°

Հաշվել ՝ ∠ABO և ∠COA
Քանի որ շրջանագծի շոշափողը ուղղահայաց է շոշափման կետից տարված շառավղին ապա <ABO=90 <COA=180-29-90=61

4. Տրված է՝ AB=12մ BO=5մ։ Գտնել CA-ն և OC-ն

BO=OC=5 քանի որ շառավիղներ են և քանի որ շրջանագծի շոշափողը ուղղահայաց է շոշափման կետից տարված շառավղին ապա AB=AC=12

5. AB ուղիղը B կետում շոշափում է O կենտրոնով և r=2,5 սմ շառավիղով շրջանագիծը: Գտնել ABO եռանկյան անկյունները, եթե AO=5 սմ:

6. Տրված է O կենտրոնով և 3,5 սմ շառավիղով շրջանագիծ: A կետն այնպիսին է, որ AO=7 սմ: A կետով տարված են այդ շրջանագծի երկու շոշափողներ: Գտնել դրանց կազմած անկյունը:

7. AB-ն և AC-ն O կենտրոնով շրջանագծին A կետից տարված շոշափողների հատվածներն են : Գտնել BAC անկյունը, եթե AO հատվածի միջնակետը գտնվում է այդ շրջանագծի վրա:

8. Տրված է A անկյանը, որի կողմերը շոշափում են O կենտրոնով և 6,78 սմ շառավղով շրջանագիծը: Հաշվել OA հատվածի երկարությունը, եթե  ∠A=60°:

Հարցեր և առաջադրանքներ։

Ճիշտ են արդյո՞ք հետևյալ պնդումները:

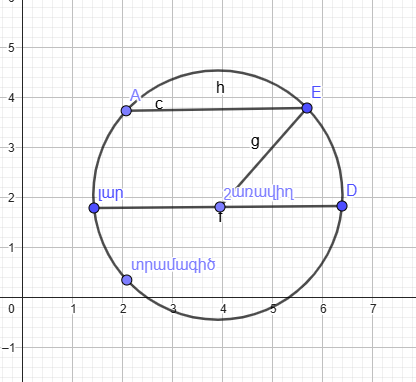
1. Եթե ուղիղը շրջանագծի շոշափողն է, ապա այն ունի շրջանագծի հետ երկու ընդհանուր կետ:
Սխալ է

2. Եթե ուղիղը շրջանագծի հետ ունի ընդհանուր կետ, ապա այն հանդիսանում է շրջանագծի հատող:
Սխալ է

3. Ուղիղն ու շրջանագիծը կարող են ունենալ միայն երկու ընդհանուր կետ:
Ճիշտ է

4.Ո՞ր ուղիղն է կոչվում շրջանագծին հատող:
Եթե ուղիղը շրջանագծի հետ ունի երկու ընդհանուր կետեր, ապա այն կոչվում է շրջանագծի հատող:

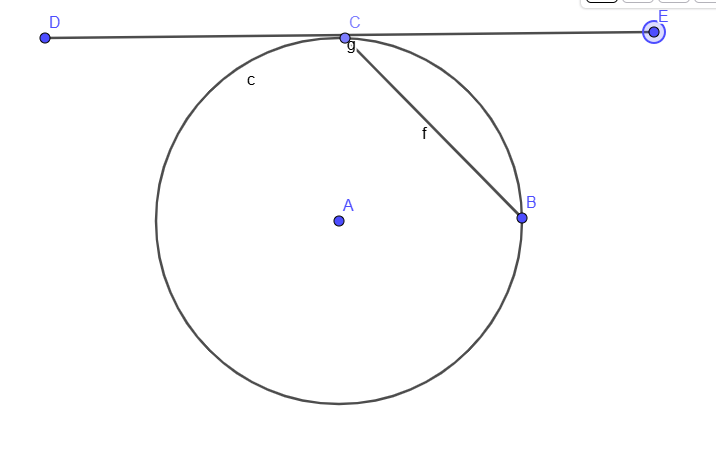
5.Ո՞ր ուղիղն է կոչվում շրջանագծի շոշափող: 
Եթե ուղիղը շրջանագծի հետ ունի մեկ ընդհանուր կետ, ապա այն կոչվում է շրջանագծի շոշափող:

6.Ո՞ր կետն է կոչվում շրջանագծի և ուղղի շոշափման կետ:
Շրջանագծի և ուղղի շոշափման կետ կոչվում է այն կետը, որը ընդանուր է համ շրջանագծին, համ ուղղին։

7. Դիցուք՝ d-ն r շառավղով շրջանագծի կենտրոնի հեռավորությունն է p ուղղից: Ինչպե՞ս են միմյանց նկատմամբ դասավորված շրջանագիծը և p ուղիղը, եթե՝

ա) r=18 սմ, d=13 սմ հատվում է
բ) r=6 սմ, d=5,6 սմ հատվում է
գ) r=7,2 սմ, d=3,7 դմ չի հատվում
դ) r=9 սմ, d=1,3 դմ չի հատվում
ե) r=6 սմ, d=60 մմ չի հատվում

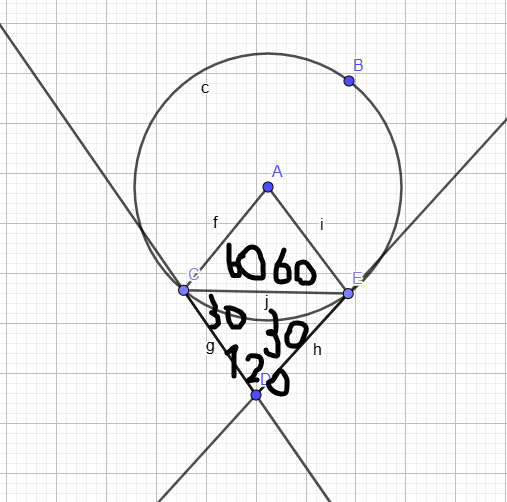
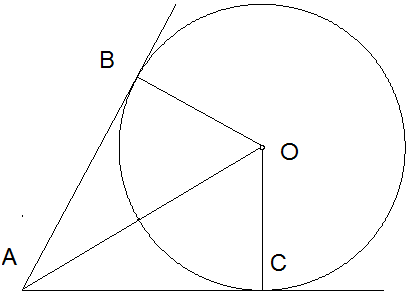
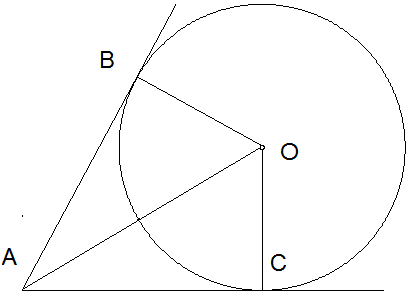
8. ABC եռանկյան մեջ AB=10սմ, ∠C=90⁰, ∠B=30⁰: Պահանջվում է տանել A կենտրոնով շրջանագիծ: Ինչպիսի՞ն պետք է լինի այդ շրջանագծի շառավիղը, որպեսզի BC ուղիղը՝

ա) շոշափի շրջանագիծը,

բ) շրջանագծի հետ չունենա ընդհանուր կետ,

գ) շրջանագծի հետ ունենա ընդհանուր կետեր:

9.Տրված է ABCD քառակուսին, որի անկյունագիծը 6 սմ է: Տանել շրջանագիծ, որի կենտրոնը լինի A–ն: Ի՞նչ երկարություն պետք է ունենա շրջանագծի շառավիղը, որպեսզի BD անկյունագիծն ընդգրկող ուղիղը լինի՝ 

ա) շրջանագծի շոշափող
Շրջանագծի շառավիղը պետք է լինի 3սմ։
բ) շրջանագծի հատող:
Շրջանագծի շառավիղը պետք է լինի 3-ից մեծ:

10. AB և CD հատվածները O կենտրոնով շրջանագծի տրամագծեր են: Հաշվեք AOD եռանկյան պարագիծը, եթե հայտնի է, որ CB = 15 սմ, AB = 14 սմ:

16/2=8
P=8+8+13=29

1.Քանի՞ համաչափության առանցք ունի հավասարասրուն  եռանկյունը։
Ունի մեկ համաչափության առանցք։

2.Ո՞ր մարմինն է կոչվում   պրիզմա ։     

3․ Քանի՞ նիստ, կող, գագաթ ունի ուղղանկյունանիստը։
6 նիստ
12 կող
8 գագաթ

4․ Խորանարդի անկյունագծի  քառակուսին երկարությունը հավասար է  48 սմ²:Գտնել խորանարդի կողի  երկարությունը։
Պատասխան՝24 սմ

5․ Գտնել տասնհինգանկյան պրիզմայի կողերի,  գագաթների, նիստերի քանակը։
Կողեր-35

Գագաթներ-30

Նիստեր-17

Հարցեր և առաջադրանքներ:

1․ Ո՞ր պատկերն է կոչվում շրջանագիծ:
Շրջանագիծ կոչվում է երկրաչափական այն պատկերը, որը կազմված է հարթության բոլոր այն կետերից, որոնք գտնվում են տրված կետից տրված հեռավորության վրա:

2. Ի՞նչ է շրջանագծի շառավիղ, տրամագիծը, լարն ու աղեղը:
Եթե լարը անցնում է շրջանագծի կենտրոնով, ապա այն կոչվում է շրջանագծի տրամագիծ:

3․ GEOGEBRA ծրագրով գծել շրջանագիծ և տանել նրա շառավիղը, տրամագիծը և լարը:

4․ Գրել լարի միջնակետով անցնող շառավղի հատկությունները:
Լարի միջնակետով անցնող շառավիղը ուղղահայաց է այդ լարին և լարը հատող և նրան ուղղահայաց շառավիղն անցնում է այդ լարի միջնակետով։

5․ Թվարկել   շրջանագծի բոլոր  տրամագծերը,   շառավիղները և  լարերը:

CK և BF տրամագծերն են
AO,KO,CO,BO, FO  շառավիղ է
BL, LE, DF լարերն են

6․ Թվարկել ստացված աղեղները:

Պատասխան՝2 աղեղ

7․ Քանի՞ անգամ է շրջանագծի տրամագիծը մեծ նրա շառավղից։
Պատասխան՝2 անգամ

8․ Ողիղը հատում է շրջանագիծը A և B կետերում։ Ի՞նչ կետերով պիտի անցնի այդ ուղիղը, որպեսզի AB հատվածն ունենա հնարավոր ամենամեծ երկարությունը։

Պատասխան՝Կենտրոնով

9․ Հաշվել CA -ն, եթե CD=8 սմ և ∠AOD=120°

Պատասխան՝CD/2=4սմ

10․AB հատվածը O կենտրոնով շրջանագծի տրամագիծն է, իսկ AC-ն և BC -ն այդ շրջանագծի հավասար լարեր են։ Գտնել AOC անկյունը։

AOC=90

Հարցեր և առաջադրանքներ։

1.Ո՞ր մարմինն է կոչվում  բուրգ։

2.GEOGEBRA ծրագրով գծիր  բուրգ։

3.Ո՞ր նիստերն են կոչվում հիմքեր, կողմնային նիստեր:
նիստերից երկուսը նրա հիմքերն են, իսկ n-ը՝ կողմնային նիստեր:

4․Գտեք վեցանկյան բուրգի կողերի, գագաթների, նիստերի քանակը,

GEOGEBRA     ծրագրով գծեք վեցանկյուն բուրգ:

կող – 12
գագաթ – 7
նիստ – 7

5․Կարո՞ղ է բուրգի կողերի թիվը լինել՝

   ա) 13      բ) 16      գ) 19։ Պատասխանը հիմնավորել։Որովհետև բաժանվում է 2-ի

6․Կարո՞ղ է լինել այնպիսի բուրգ, որն ունի ՝

   ա) 9 նիստ,         բ)  9 կող։ Պատասխանը հիմնավորել։Քանի որ 9-ից հանել մեկ հնարավոր է։

7․ Ինչպե՞ս է կոչվում այն բուրգը, եթե այն ունի

   ա) 13 նիստ     բ) 10 գագաթ    գ) 12 կող։

ա) 13 նիստ – տասներկուանկյուն բուրգ
բ) 10 գագաթ –  իննանկյուն բուրգ 
գ) 12 կող – վեցանկյուն բուրգ։

8․Քառանկյուն բուրգի հիմքը 64 սմ պարագծով քառակուսի է, իսկ կողմնային նիստերը

     հավասարակողմ եռանկյուններ են։ Գտեք բուրգի կողմնային կողերը։
64։4=16

Հարցեր և առաջադրանքներ։

1.Որ մարմինն է կոչվում պրիզմա:

2.GEOGEBRA ծրագրով գծիր պրիզմա:

3.Որ նիստերն են կոչվում հիմքեր, կողմնային նիստեր:
նիստերից երկուսը նրա հիմքերն են, իսկ n-ը՝ կողմնային նիստեր:

4.Որ պրիզման է կոչվում ուղիղ պրիզմա։
Եթե պրիզմայի կողմնային կողերը ուղղահայաց են հիմքերին, ապա այն կոչվում է ուղիղ պրիզմա: 

5.GEOGEBRA ծրագրով գծիր ուղիղ պրիզմա:

6.Որ պրիզման է կոչվում թեք պրիզմա։

7․GEOGEBRA ծրագրով գծիր թեք պրիզմա:

8․Գտեք վեցանկյան պրիզմայի կողերի, գագաթների, նիստերի քանակը,GEOGEBRA ծրագրով գծեք վեցանկյան պրիզմա:

9․Կարող է պրիզմայի կողերի թիվը լինել՝

ա)13
բ)14
գ)18

10․Կարող է պրիզմայի նիստերի թիվը լինել՝

ա)13
բ)14
գ)18։
Նիստերի թիվը լինում է 8

11․ Ինչ բազմանկյուն է պրիզմայի հիմքը, եթե պրիզման ունի ՝

ա)15 կող հնգանկյուն
բ)11 նիստ
գ) 10 գագաթ։

Հարցեր և առաջադրանքներ։

1․ Ո՞ր մարմինն է կոչվում ուղղանկյունանիստ։ GEOGEBRA ծրագրով գծել ուղղանկյունանիստ։

2․ Ի՞նչ երկրաչափական պատկերներից է կազմված ուղղանկյունանիստը։
հիմք և կոմնային նիստ

3․ Ո՞ր մարմինն է կոչվում խորանարդը։ GEOGEBRA ծրագրով գծել խորանարդ։

4․ Քանի՞ նիստ, կող, գագաթ ունեն ուղղանկյունանիստն ու խորանարդը։
6 նիստ
12 կող
8 գագաթ

5․ Որո՞նք են ուղղանկյունանիստի չափումները։
Ուղղանկյունանիստի ընդհանուր գագաթով երեք կողերի երկարությունները անվանում են ուղղանկյունանիստի չափսեր՝ երկարություն, լայնություն, բարձրություն:

6․ Համեմատել խորանարդը և ուղղանկյունանիստը։
Այն ուղղանկյունանիստը, որի բոլոր կողերը հավասար են, կոչվում է խորանարդ:

7․ Տրված է հետևյալ ուղղանկյունանիստը:

Ո՞րն է ուղղանկյունանիստի անկյունագծի հաշվման բանաձևը:  Ընտրել ճիշտ բանաձև(եր)ը:

• KM²=KN²+NM²
• AM²=AD²+DC²+CM²
• BN²=BD²+DN²

8․ Հայտնի են ուղղանկյունանիստի նույն գագաթից ելնող կողերի երկարությունները՝  10 սմ,  2 սմ  և  4 սմ: Գտնել  ուղղանկյունանիստի անկյունագծի քառակուսու երկարությունը:  
10²+2²+4²=100+4+16=120

9․ Հայտնի են ուղղանկյունանիստի հիմքի կողերի երկարությունները՝ 16 սմ, 24 սմ և  ուղղանկյունանիստի  անկյունագծի երկարության քառակուսին՝ 857: Գտնել ուղղանկյունանիստի բարձրությունը:
857=16²+24²+c²
c²=857-256-576=25
c²=25
c=12,5

10․ Որոշել խորանարդի d անկյունագիծը, եթե նրա մի նիստի մակերեսը S=49 սմ²է:
d=49*6

Հարցեր և առաջադրանքներ։

1․ Ո՞ր պատկերն է կոչվում տարածական մարմին կամ տարածական պատկեր։

2․ GEOGEBRA ծրագրով գծել տարածական մարմին։

3․ Ի՞նչ է բազմանիստը։
Նիստերի կողմերը կոչվում են բազմանիստի կողեր:

4․ Ո՞ր պատկերն է կոչվում զուգահեռանիստ, GEOGEBRA ծրագրով գծել զուգահեռանիստ։

5․ Զուգահեռանիստը քանի՞ նիստ, քանի՞ կող, քանի՞ գագաթ ունի։
6 նիստ
8 գագաթ
12 կող

6․ Բազմանիստների և նրանց տարրերի մասին բերված պնդումներից (սահմանումներից) ո՞րն է ճիշտ: Ընտրել ճիշտ տարբերակ(ներ)ը:

Եթե տարածական մարմնի մակերևույթը կազմված է ուղղանկյուններից, ապա այն կոչվում է բազմանիստ:

Բազմանիստի մակերևույթը կազմող բազմանկյունները կոչվում են բազմանիստի նիստեր:

Նիստերի կողմերը կոչվում են բազմանիստի կողեր:

Եթե տարածաչափական մարմնի մակերևույթը բաղկացած է բազմանկյուններից, ապա մարմինը բազմանիստ է:

7․ Զուգահեռանիստի մասին թվարկված պնդումներից ո՞րն է ճիշտ: Ընտրել ճիշտ պնդումը:

Զուգահեռանիստի հիմքը զուգահեռագիծ է:

Զուգահեռանիստ կոչվում է այն պրիզման, որի կողմնային նիստերը չորս ուղղանկյուններ են:

Զուգահեռանիստի նիստերը վեց ուղղանկյուններ են:

8․ Բերվածնկարներից ո՞րն է զուգահեռանիստը: Նշել  ճիշտ պատասխանը:
1․

2․

3․

երորդ նկարն է

9․ Գրել զուգահեռանիստի հատկությունները։

Զուգահեռանիստի հանդիպակաց նիստերը զուգահեռ են և հավասար:
Զուգահեռանիստի բոլոր չորս անկյունագծերը հատվում են միևնույն կետում և այդ կետում կիսվում են: 

10․ ABCDA₁B₁C₁D₁ զուգահեռանիստի մեջ գտնել B₁C₁ -ը և DC-ն, եթե BC=7 սմ, A₁B₁=5 սմ:

Առաջադրանքներ։

1. O կետը AL հատվածը բաժանում է երկու հավասար մասերի: Գտնել  հատվածի միջնակետի նկատմամբ համաչափ կետեր:

E-F
D-H
C-I
B-J
A-K

2. Տրված է AL հատվածը: Գտնել D կետի նկատմամբ համաչափ կետերը:

C-E
B-F
A-G

3. Ո՞ր կետն է C կետին համաչափ՝ (0;−4) կետի նկատմամբ:

C=(-3;-4)

4. Գտնել Оx առանցքի նկատմամբ B կետին համաչափ կետը:

A-(4;3)

5․ Կոորդինատային հարթության վրա կառուցիր հետևյալ գագաթներով եռանկյունը` A(9; 3), B(3;−9) և C(−9; −3)։ Կառուցել A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> եռանկյունը, որը համաչափ է տրվածին` y=3 ուղղի նկատմամբ: Գրել  A₁B₁C₁ եռանկյան գագաթների կոորդինատները:

6․ Կոորդինատային հարթության վրա գծիր քառանկյուն, որի գագաթները հետևյալ կետերն են՝

A(18; 6), B(6; −18), C(−18; −6) և D(−6; 18)։ Գծել A₁B₁C₁D₁ քառանկյունը, որը համաչափ է տրված քառանկյանը՝ (0;0) կետի նկատմամբ: Գրել  A₁B₁C₁D₁ քառանկյան գագաթները:

7․ Նշել այն պատկերները, որոնք ունեն համաչափության կենտրոն:

• Իննանկյուն ոչ
• Սեղան այո
• Քառակուսի այո
• Ուղղանկյուն այո

8․ Նշել այն պատկերները, որոնք ունեն համաչափության առանցք: 

• Շրջան այո
• Քառանկյուն այո
• Եռանկյուն այո
• Շեղանկյուն այո

9․ Նշել այն տառերը և թվերը, որոնց տեսքն ունի համաչափության առանցք: