Հարցեր և առաջադրանքներ։

1․ Ո՞ր  շրջանագիծն  է  կոչվում  բազմանկյանը  արտագծյալ:
Եթե բազմանկյան բոլոր գագաթները գտնվում են շրջանագծի վրա, ապա շրջանագիծը կոչվում է այդ բազմանկյան արտագծյալ շրջանագիծ:  

2․ Քանի՞  շրջանագիծ  կարելի  է  արտագծել  տրված  եռանկյանը:
1

3․ Հնարավո՞ր  է  արդյոք  ցանկացած  քառանկյան  արտագծել  շրջանագիծ: 
ոչ

4․ Ի՞նչ  հատկություն  ունի  շրջանագծին  ներգծված  քառանկյունը:
Ցանկացած ներգծյալ քառանկյուն հանդիպակաց անկյունների գումարը 180⁰ է:

5․Սեղանին արտագծված է շրջանագիծ: Հաշվիր սեղանի մյուս անկյունները, եթե անկյուններից մեկը՝ F=10° է:

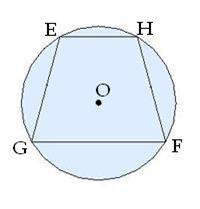
Ցանկացած ներգծյալ քառանկյան հանդիպակաց անկյունների գումարը 180⁰ է:
E+F=180 ապա E=170
Ցանկացած սեղանի սրունքին առընթեր անկյունների գումարը 180° է:
Քանի որ E=10 ապա G=170

6․ Գտնել B և D անկյունները։

Ցանկացած ներգծյալ քառանկյան հանդիպակաց անկյունների գումարը 180⁰ է:
Քանի որ R=85 ապա D=95
Քանի որ I=117 ապա B=63

7․ O կենտրոնով շրջանագծին ներգծված է ZXY եռանկյունն այնպես, որ ZX-ը  տրամագիծ է։ ZY աղեղի աստիճանային չափը հավասար է 104⁰ -ի։ Գտնել ZXY եռանկյան անկյունները։

Կիսաշրջանագծի վրա հենված ներգծյալ անկյունը 90° է դրանից => Y=90^o
Ներգծյալ անկյունը չափվում է այն աղեղի կեսով, որի վրա նա հենվում է՝ =>
x=ZY/2=52 Z=180-90-52=38

8․ Օգտվելով գծագրից, գտնել ∠ B-ը։

Կիսաշրջանագծի վրա հենված ներգծյալ անկյունը 90° է դրանից => C=90^o
B=180-90-46=44

9․ Գտնել ∠ R-ը և ∠B-ն։

Ցանկացած ներգծյալ քառանկյան հանդիպակաց անկյունների գումարը 180⁰ է:
Քանի որ A=92 ապա R=88
Քանի որ E=74 ապա B=106

10․ ABC եռանկյանը արտագծված է շրջանագիծ։ Գտնել այդ շրջանագծի շառավիղը, եթե AC=24 սմ, ∠A=60⁰, ∠B=30⁰:
r=AB/2 քանի որ ∠B=30 է , եռանկյուն ABC ուղղանկյուն եռանկյուն է => AC=AB/2 => r=6

11. Արդյոք կարելի՞ է տրված ABCD քառանկյանը արտագծել շրջանագիծ, եթե
ա)∠A=64⁰, ∠ B=95⁰, ∠C=106⁰
բ) ∠A=72⁰, ∠B=69⁰, ∠D=111⁰
գ) ∠A=90⁰, ∠C=90⁰, ∠D=80⁰: